- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Ultima modifica 2025-06-01 06:06.
La sottrazione è semplicemente sottrarre un numero da un altro. È facile sottrarre un numero intero da un altro, ma la sottrazione può essere complicata se stai sottraendo frazioni o decimali. Una volta compresa la sottrazione, sarai in grado di utilizzare concetti matematici più complessi e di aggiungere, moltiplicare e dividere i numeri più facilmente.
Fare un passo
Metodo 1 di 6: sottrarre numeri interi grandi prendendo in prestito

Passaggio 1. Annotare un numero elevato
Ad esempio, vuoi risolvere 32 - 17. Scrivi prima 32.

Passaggio 2. Scrivi il numero più piccolo proprio sotto di esso
Assicurati di posizionare i valori delle decine e delle unità nelle colonne corrette, in modo che 3 di 32 sia direttamente sopra 1 di 17 e 2 di 32 sia direttamente sopra 7 di 17.
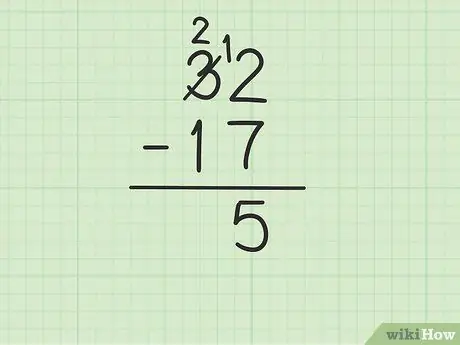
Passaggio 3. Sottrarre il numero in alto nella colonna delle unità dal numero in basso
Tuttavia, questo può diventare complicato se il numero in basso è maggiore del numero in alto. In questo caso, 7 è maggiore di 2. Ecco cosa devi fare:
- Devi prendere in prestito dal numero 3 di 32 (noto anche come raggruppamento), per trasformare 2 in 12.
- Cancella il numero 3 su 32 e sostituiscilo con il numero 2, mentre il numero 2 diventa 12.
- Ora puoi sottrarre 12 - 7, che è uguale a 5. Scrivi 5 sotto i due numeri che stai sottraendo in modo che siano nella colonna delle unità della nuova riga.
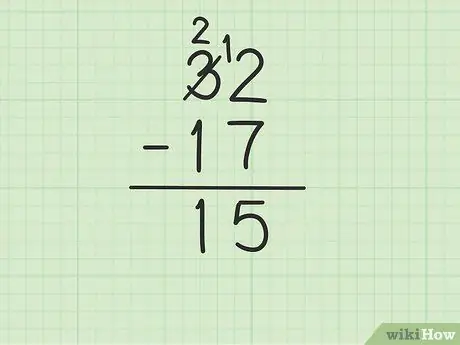
Passaggio 4. Sottrarre il numero in alto nella colonna delle decine dal numero in basso
Ricorda che 3 è diventato 2. Ora sottrai 1 da 17 da 2 sopra per ottenere (2-1) 1. Scrivi 1 sotto, nella colonna delle decine, a sinistra di 5 nella colonna delle unità. Scrivi 15. Cioè 32 - 17 = 15.
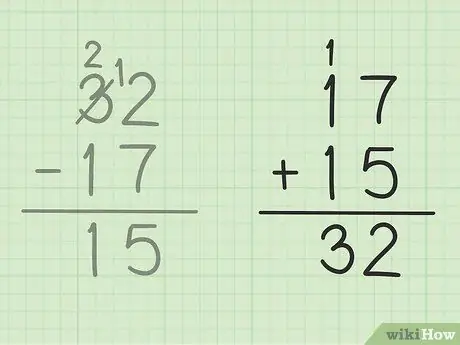
Passaggio 5. Controlla il tuo lavoro
Se vuoi assicurarti di aver sottratto due numeri correttamente, tutto ciò che devi fare è sommare la tua risposta con il numero più piccolo per ottenere un numero grande. In questo problema, devi aggiungere la tua risposta, 15 al numero minore di sottrazione, 17. 15 + 17 = 32, in modo che la tua risposta sia corretta. Sicuro!
Metodo 2 di 6: sottrai piccoli numeri interi
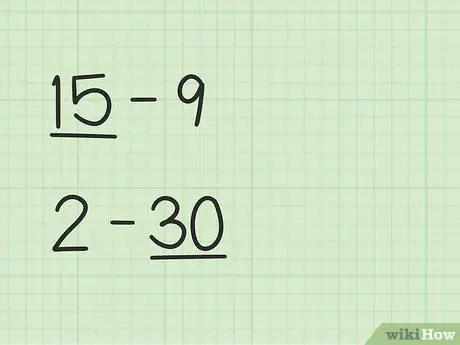
Passaggio 1. Trova il numero più grande
Problemi come 15 -9 avranno un modo diverso di 2 - 30.
- Nelle domande 15-9, il primo numero, 15, è maggiore del secondo numero, 9.
- Nelle domande 2-30, il secondo numero, 30, è maggiore del primo numero, 2.
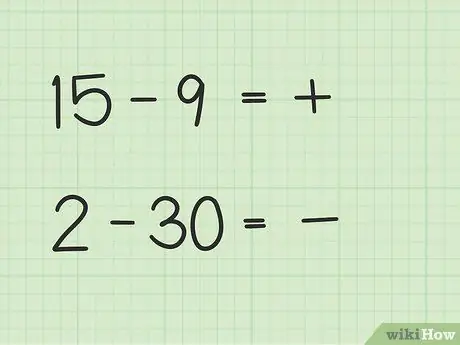
Passaggio 2. Decidi se la tua risposta sarà positiva o negativa
Se il primo numero è maggiore, la risposta è positiva. Se il secondo numero è maggiore, la risposta è negativa.
- Nella prima domanda, 15 - 9, la tua risposta è positiva perché il primo numero è maggiore del secondo numero.
- Nella seconda domanda, 2 - 30, la tua risposta è negativa perché il secondo numero è maggiore del primo.
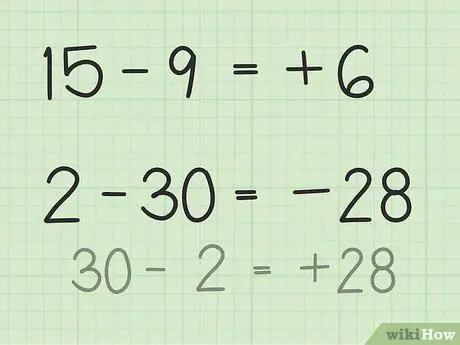
Passaggio 3. Trova la differenza tra due numeri
Per sottrarre due numeri, devi immaginare la differenza tra i due numeri e calcolare i numeri tra di loro.
- Per le domande 15 - 9, immagina una pila di 15 fiches da poker. Butta via 9 gettoni e solo 6. Quindi, 15 - 9 = 6. Puoi anche immaginare una linea dei numeri. Pensa ai numeri da 1 a 15, quindi scarta o restituisci 9 unità in modo da ottenere 6.
- Per le domande da 2 a 30, il modo più semplice per risolverlo è invertire il numero e rendere il risultato negativo dopo aver sottratto. Quindi, 30 - 2 = 28, quindi 28 e 30 hanno una differenza di 2. Ora, rendi il risultato negativo perché hai già determinato che la risposta è negativa perché il secondo numero è maggiore del primo numero. Quindi, 2 - 30 = -28.
Metodo 3 di 6: sottrazione di decimali
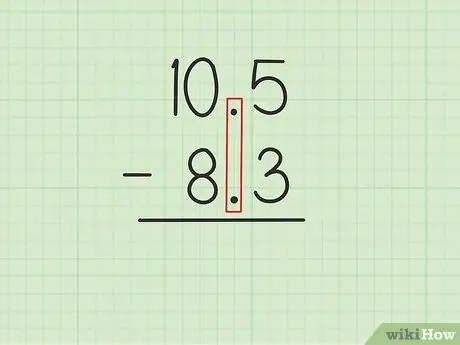
Passaggio 1. Scrivi il numero più grande sul numero più piccolo con i punti decimali allineati
Supponiamo di voler risolvere i seguenti problemi: 10, 5 - 8, 3. Scrivi 10, 5 su 8, 3 in modo che le virgole dei due numeri siano parallele., 5 di 10, 5 deve essere direttamente sopra, 3 di 8, 3 e 0 di 10, 5 devono essere sopra 8 di 8, 3.
Se hai un problema perché i due numeri non hanno lo stesso numero dopo la virgola, scrivi 0 nello spazio vuoto finché la somma dei numeri non è la stessa. Ad esempio, il problema è 5, 32 - 4, 2, puoi scriverlo come 5, 32 - 4, 2 0. Questo non cambierà il valore del secondo numero, ma renderà più facile la sottrazione dei due numeri.

Passaggio 2. Sottrai il numero in alto nella colonna delle decine dal numero sottostante
In questo caso devi sottrarre 3 da 5. 5 - 3 = 2, quindi devi scrivere 2 sotto 3 di 8, 3.
Assicurati di inserire un punto decimale nella risposta, in modo che sia scritto, 2

Passaggio 3. Sottrarre il numero sopra la colonna delle unità dal numero sottostante
Devi sottrarre 8 da 0. Prendi in prestito 1 dalla parte delle decine per cambiare 0 in 10 e sottrai 10 - 8 per ottenere 2. Puoi anche contare 10 - 8 senza prendere in prestito perché non ci sono numeri nella seconda colonna delle decine. Scrivi la risposta sotto 8, a sinistra della virgola.

Passaggio 4. Annota il risultato finale
Il tuo risultato finale è 2, 2.

Passaggio 5. Controlla il tuo lavoro
Se vuoi assicurarti che la tua sottrazione decimale sia corretta, tutto ciò che devi fare è sommare la tua risposta con il numero più piccolo per ottenere il numero più grande. 2, 2 + 8, 3 = 10, 5, quindi hai finito.
Metodo 4 di 6: sottrarre frazioni

Passaggio 1. Allineare il denominatore e il numeratore della frazione
Supponiamo di voler risolvere i problemi 13/10 - 3/5. Scrivi il problema in modo che i due numeratori 13 e 3 e i denominatori 10 e 5 siano opposti. Questi due numeri sono separati da un segno di sottrazione. Questo ti aiuterà a visualizzare il problema e a risolverlo più facilmente.

Passaggio 2. Trova il minimo comune denominatore
Il minimo comune denominatore è il numero più piccolo che può essere diviso per due numeri. In questo esempio, devi trovare il minimo comun denominatore divisibile per 10 e 5. Scoprirai che 10 è il minimo comun denominatore per entrambi i numeri perché 10 è divisibile per 10 e 5.
Nota che il minimo comune denominatore di due numeri non è sempre uno di loro. Ad esempio, il minimo comune denominatore per 3 e 2 è 6 perché 6 è il numero più piccolo che può essere diviso per due numeri
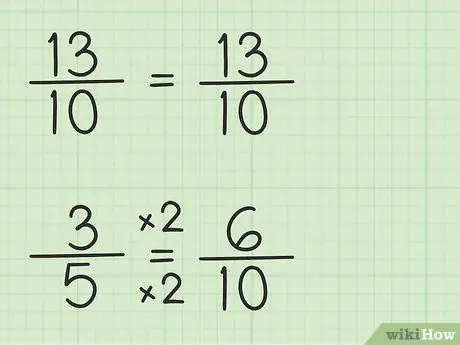
Passaggio 3. Annota le frazioni usando lo stesso denominatore
La frazione 13/10 può essere scritta allo stesso modo perché il denominatore è 10, il minimo comun denominatore, che è 10, moltiplicato per 1. Tuttavia, la frazione 3/5 deve essere riscritta perché il denominatore è 5, il minimo comun denominatore, che è 10, per 2. Quindi la frazione 3/5 deve essere moltiplicata per 2/2 per ottenere il denominatore 10, quindi 3/5 x 2/2 = 6/10. Hai trovato la frazione equivalente. 3/5 equivale a 6/10 anche se 6/10 permette di sottrarre il primo numero, 13/10.
Scrivi una nuova domanda come questa: 13/10 - 6/10
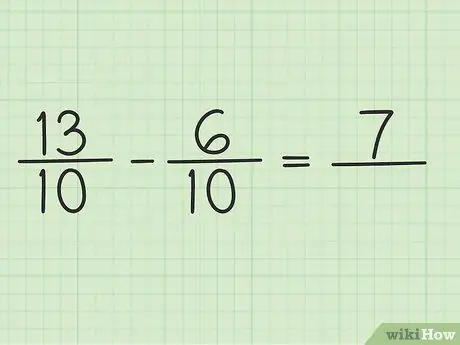
Passaggio 4. Sottrarre il numeratore a due numeri
Sottrai solo 13 - 6 in modo che il risultato sia 7. Non puoi cambiare il denominatore della frazione.
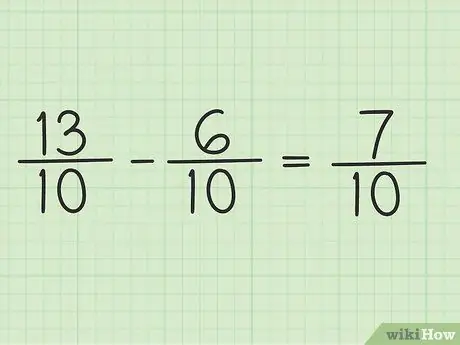
Passaggio 5. Scrivi il nuovo numeratore sullo stesso denominatore per ottenere il risultato finale
Il nuovo numeratore è 7. Entrambe le frazioni hanno un denominatore di 10. Il risultato finale è 7/10.
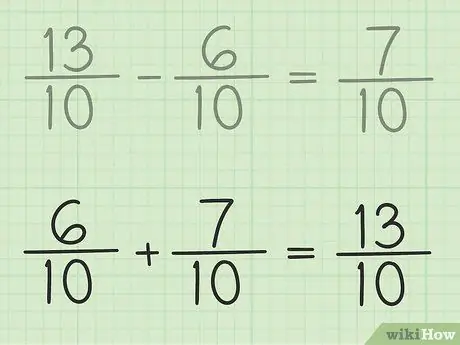
Passaggio 6. Controlla il tuo lavoro
Se vuoi assicurarti di sottrarre la frazione correttamente, somma la tua risposta e la frazione più piccola in modo che il risultato sia una frazione più grande. 7/10 + 6/10 = 13/10. È finito.
Metodo 5 di 6: sottrarre frazioni da numeri interi

Passaggio 1. Annotare il problema
Ad esempio, supponiamo di voler risolvere il seguente problema: 5 -. Scrivilo.
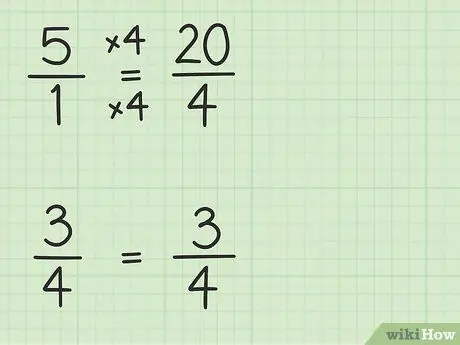
Passaggio 2. Converti numeri interi in frazioni che hanno lo stesso denominatore delle altre frazioni
Convertirai 5 in una frazione con denominatore 4 per poter sottrarre due numeri. Quindi devi pensare a 5 come una frazione di 5/1. Quindi, puoi moltiplicare il numeratore e il denominatore della nuova frazione per 4 per rendere uguali i denominatori dei due numeri. Quindi 5/1 x 4/4 = 20/4. Questa frazione è uguale a 5, ma ti permette di sottrarre due numeri.
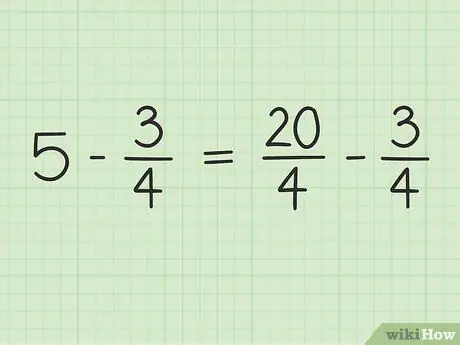
Passaggio 3. Riscrivi il problema
Il nuovo problema si può scrivere così: 20/4 - 3/4.
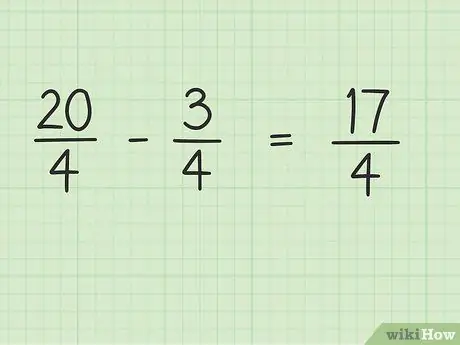
Passaggio 4. Sottrai il numeratore della frazione, mentre il denominatore rimane lo stesso
Ora, sottrai 20 per 3 per ottenere il risultato finale. 20 - 3 = 17, quindi 17 è il nuovo numeratore. Puoi lasciare il denominatore lo stesso.
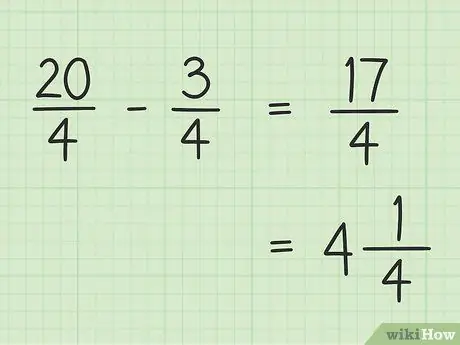
Passaggio 5. Annota il risultato finale
Il tuo risultato finale è 17/4. Se vuoi scriverlo come un numero misto, dividi 17 per 4 in modo che il risultato sia 4 e il resto sia 1, in modo che il tuo 17/4 finale sia uguale a 4.
Metodo 6 di 6: Sottrazione di variabili
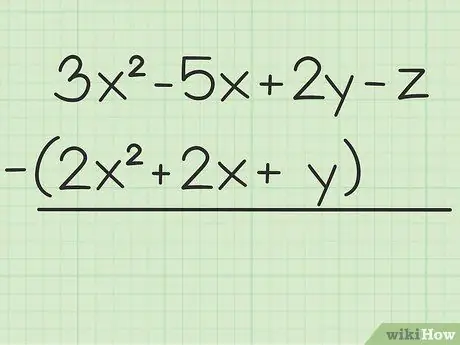
Passaggio 1. Annota il problema che vuoi risolvere
Ad esempio la seguente domanda: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Scrivi il primo insieme di variabili sul secondo.
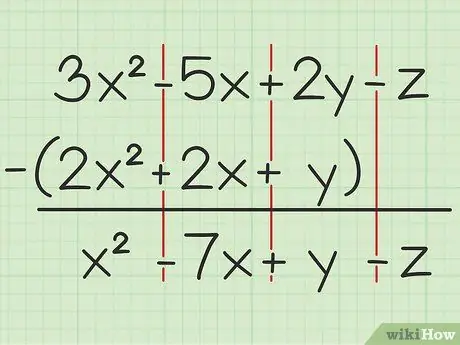
Passaggio 2. Sottrarre le stesse variabili
Se incontri una variabile, puoi solo aggiungere o sottrarre la stessa variabile e che è scritta con lo stesso grado di quadrato. Ciò significa che puoi sottrarre 4x2 da 7x2, ma non può sottrarre 4x da 4y. Quindi, puoi suddividere il problema in questo modo:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
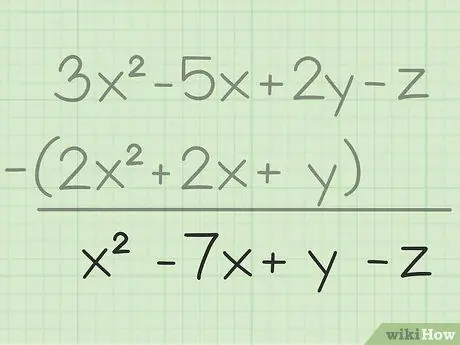
Passaggio 3. Annota il risultato finale
Hai sottratto tutte le stesse variabili, tutto ciò che devi fare è scrivere il risultato finale che conterrà tutte le variabili che hai sottratto. Ecco il risultato finale:






