- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:17.
- Ultima modifica 2025-01-23 12:21.
La gravità è una delle forze fondamentali in fisica. L'aspetto più importante della gravità è che è universale: tutti gli oggetti hanno una forza gravitazionale che attrae altri oggetti. L'entità della forza gravitazionale dipende dalla massa e dalla distanza tra i due oggetti.
Fare un passo
Parte 1 di 2: calcolo della forza di gravità tra due oggetti

Passaggio 1. Definire l'equazione per la forza gravitazionale che attira un oggetto, Fgrave = (Gm1m2)/D2.
Per poter calcolare la forza gravitazionale di un oggetto, questa equazione tiene conto anche delle masse dei due oggetti e della loro distanza l'uno dall'altro. Le variabili dell'equazione sono descritte di seguito.
- Fgrave è la forza gravitazionale
- G è la costante gravitazionale universale 6.673 x 10-11 Nm2/kg2
- m1 è la massa del primo oggetto
- m2 è la massa del secondo oggetto
- d è la distanza tra i centri dei due oggetti
- A volte trovi la lettera r invece di d. Questi due simboli rappresentano la distanza tra i due oggetti.

Passaggio 2. Utilizzare le unità metriche appropriate
Per questa equazione, è necessario utilizzare le unità metriche. La massa dell'oggetto deve essere in chilogrammi (kg) e la distanza tra gli oggetti deve essere in metri (m). È necessario convertire queste unità in unità metriche prima di procedere

Passaggio 3. Determinare la massa dell'oggetto in questione
Per piccoli oggetti, puoi pesarli per determinarne il peso in chilogrammi. Per oggetti di grandi dimensioni, puoi cercare la massa approssimativa su un tavolo o su Internet. Nei problemi di fisica, di solito viene detta la massa dell'oggetto.

Passaggio 4. Misurare la distanza tra i due oggetti
Se stai cercando di calcolare la forza gravitazionale tra un oggetto e la terra, devi sapere quanto dista questo oggetto dal centro della terra.
- La distanza dalla superficie terrestre al centro della terra è di circa 6,38 x 106 m.
- Puoi cercare tabelle o altre fonti su Internet che ti dicono la distanza approssimativa dal centro della terra agli oggetti a varie altezze sulla superficie terrestre.

Passaggio 5. Completa il calcolo
Se hai definito le variabili nell'equazione, sentiti libero di inserirle per risolverle. Assicurati che tutte le variabili siano in unità metriche e siano correttamente ridimensionate. La massa deve essere in chilogrammi e la distanza in metri. Risolvere equazioni nell'ordine corretto dei calcoli.
- Ad esempio, determina la forza gravitazionale di una persona la cui massa è di 68 kg sopra la superficie terrestre. La massa della Terra è 5,98 x 1024 kg.
- Assicurati che tutte le variabili siano nelle unità corrette. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6,673 x 10-11 Nm2/kg2e d = 6, 38 x 106 m
- Scrivi la tua equazione: Fgrave = (Gm1m2)/D2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Moltiplicare le masse dei due oggetti presi in considerazione. 68 x (5, 98 x 1024) = 4,06 x 1026
- Moltiplicare il risultato m1 e m2 con la costante gravitazionale G. (4,06 x 1026) x (6,67 x 10-11) = 2.708 x 1016
- Eleva al quadrato la distanza tra i due oggetti. (6, 38 x 106)2 = 4,07 x 1013
- Condividi risultato G x m1 x m2 dalla distanza al quadrato per ottenere la forza gravitazionale in Newton (N). 2, 708 x 1016/4, 07 x 1013 = 665 N
- La sua forza gravitazionale è di 665 N.
Parte 2 di 2: Calcolo della forza di gravità sulla Terra

Passaggio 1. Comprendi la seconda legge di Newton, F = ma
La seconda legge di Newton afferma che l'accelerazione di un oggetto è direttamente proporzionale alla forza risultante che agisce su di esso e inversamente proporzionale alla sua massa. In altre parole, se una forza che agisce su un oggetto è maggiore della forza che agisce nella direzione opposta, l'oggetto si muoverà con la forza più forte.
- Questa legge può essere riassunta dall'equazione F = ma, dove F è la forza, m è la massa dell'oggetto e a è l'accelerazione.
- Grazie a questa legge, possiamo calcolare la forza gravitazionale di tutti gli oggetti sulla superficie terrestre, utilizzando la nota accelerazione di gravità.
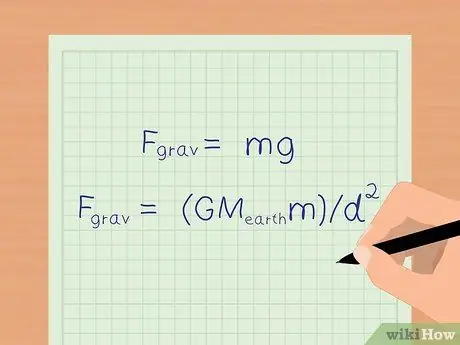
Passaggio 2. Trova l'accelerazione dovuta alla gravità terrestre
Sulla terra, la forza di gravità fa sì che tutti gli oggetti accelerino di 9,8 m/s2. Sulla superficie terrestre, possiamo usare un'equazione semplificata: Fgrave = mg per calcolare la forza gravitazionale.
Se vuoi conoscere un numero più preciso di forze gravitazionali, puoi comunque utilizzare la formula nel passaggio precedente, Fgrave = (GMterram)/d2 per determinare la forza gravitazionale.

Passaggio 3. Utilizzare le unità metriche appropriate
Per questa equazione, è necessario utilizzare le unità metriche. La massa dell'oggetto deve essere in chilogrammi (kg) e la distanza tra gli oggetti deve essere in metri (m). È necessario convertire queste unità in unità metriche prima di procedere.

Passaggio 4. Determinare la massa dell'oggetto in questione
Per piccoli oggetti, puoi pesarli per determinarne il peso in chilogrammi. Per oggetti di grandi dimensioni, puoi cercare la massa approssimativa su un tavolo o su Internet. Nei problemi di fisica, di solito viene detta la massa dell'oggetto.

Passaggio 5. Completa il calcolo
Se hai definito le variabili nell'equazione, sentiti libero di inserirle per risolverle. Assicurati che tutte le variabili siano in unità metriche e siano correttamente ridimensionate. La massa deve essere in chilogrammi e la distanza in metri. Risolvere equazioni nell'ordine corretto dei calcoli.
- Proviamo a utilizzare l'equazione nel passaggio precedente e vediamo quanto sono vicini i risultati. Determina la forza gravitazionale di una persona con una massa di 68 kg sulla superficie terrestre.
- Assicurati che tutte le variabili siano nelle unità corrette: m = 68 kg, g = 9,8 m/s2.
- Scrivi la formula. Fgrave = mg = 68*9, 8 = 666 N.
- Usando la formula F = mg la forza gravitazionale è 666 N, mentre il risultato della formula nel passaggio precedente è 665 N. Come puoi vedere, i due risultati sono quasi gli stessi.
Suggerimenti
- Queste due formule dovrebbero dare la stessa risposta, ma la formula più breve e più semplice è più facile da usare quando si discute di oggetti sulla superficie di un pianeta.
- Usa la prima formula se non conosci l'accelerazione di gravità su un pianeta, o stai calcolando la forza gravitazionale tra due oggetti molto grandi, come la luna o i pianeti.






