- Autore Jason Gerald [email protected].
- Public 2024-02-01 14:13.
- Ultima modifica 2025-01-23 12:21.
Lo spostamento in fisica denota un cambiamento nella posizione di un oggetto. Quando calcoli lo spostamento, calcoli la distanza di un oggetto in base alle sue posizioni iniziale e finale. La formula che usi per calcolare lo spostamento dipende dalla variabile data al problema. Seguire questi passaggi per calcolare lo spostamento.
Fare un passo
Parte 1 di 5: Calcolo dello spostamento risultante

Passaggio 1. Utilizzare la formula di spostamento risultante se l'unità di distanza viene utilizzata per indicare le posizioni di partenza e di arrivo
Sebbene la distanza sia diversa dallo spostamento, il problema dello spostamento risultante cerca quanti chilometri o metri ha percorso l'oggetto. Utilizzerai questa unità di misura per calcolare lo spostamento e la distanza dalla posizione di un oggetto rispetto al suo punto di partenza.
- La formula di spostamento risultante è scritta come: S = x²+y². S è spostamento. X è la prima direzione di movimento dell'oggetto e Y è la seconda direzione di movimento dell'oggetto. Se il tuo oggetto si muove solo in una direzione, allora Y = 0.
- Un oggetto può muoversi solo in un massimo di due direzioni perché lo spostamento lungo un asse nord/sud o est/ovest è considerato un movimento neutro.

Passaggio 2. Collega i punti in ordine di movimento ed etichettali dalla A alla Z
Usa un righello per tracciare una linea retta da un punto all'altro.
- Ricorda anche di collegare il punto di partenza con il punto di arrivo utilizzando una linea retta. Questo è lo spostamento che calcoleremo.
- Ad esempio, se un oggetto si sposta a est di 300 me a nord di 400 m, formerà un triangolo rettangolo. AB sarà la prima gamba del triangolo e BC sarà la seconda gamba. AC sarà l'ipotenusa del triangolo e la sua grandezza è lo spostamento dell'oggetto. In questo esempio, le due direzioni sono est e nord.

Passaggio 3. Immettere i valori per x² e y²
Ora che conosci le due direzioni di movimento del tuo oggetto, inserisci i valori nelle variabili appropriate.
Ad esempio, x = 300 e y = 400. La tua formula dovrebbe assomigliare a questa: S = 300² + 400²
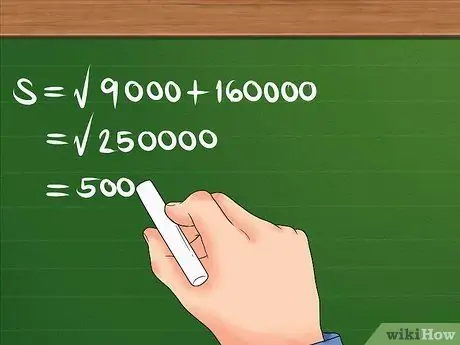
Passaggio 4. Calcola la formula utilizzando l'ordine delle operazioni
Prima i quadrati 300 e 400, poi sommali e trova la radice quadrata della somma.
Ad esempio: S = 90000 + 160000. S = 250000. S = 500. Ora sai che lo spostamento è di 500 m
Parte 2 di 5: quando si conoscono velocità e tempo

Passaggio 1. Utilizzare questa formula quando il problema indica la velocità di un oggetto e il tempo necessario
Alcuni problemi di matematica non ti diranno quanto lontano o quanto velocemente si sta muovendo un oggetto. Puoi calcolare lo spostamento usando questa grandezza di tempo e velocità.
-
In questo caso la formula diventa: S = 1/2(u + v)t.
U = velocità iniziale dell'oggetto, ovvero quanto velocemente l'oggetto inizia a muoversi in una certa direzione. V = velocità finale dell'oggetto, o quanto velocemente l'oggetto si sta muovendo verso la sua posizione finale. T = il tempo impiegato dall'oggetto per raggiungere la sua posizione finale.
- Esempio: un'auto percorre la strada per 45 secondi (tempo necessario). L'auto sta girando verso ovest a 20 m/s (velocità iniziale) e alla fine della strada la sua velocità è 23 m/s (velocità finale). Calcola lo spostamento in base a questi fattori.

Passaggio 2. Immettere la velocità e il tempo richiesti nelle variabili appropriate
Ora che sai quanto lontano si sta muovendo l'auto, quanto velocemente si sta muovendo l'auto all'inizio e alla fine, puoi trovare la distanza dalla posizione di partenza alla posizione finale.
La tua formula dovrebbe assomigliare a questa: S = 1/2(20 + 23)45

Passaggio 3. Calcola la formula dopo aver inserito i valori nella posizione corretta
Ricordarsi di seguire l'ordine delle operazioni, altrimenti gli spostamenti risulteranno in valori molto diversi.
- Per questa formula, non importa se si scambiano accidentalmente le velocità iniziale e finale. Dato che prima dovrai sommare questi numeri, non importa dove si trovano tra parentesi. Tuttavia, per altre formule, scambiando le velocità iniziale e finale si otterranno valori di spostamento diversi.
- La tua formula dovrebbe assomigliare a questa: S = 1/2(43)45. Prima dividi 43 per 2, che risulta in 21, 5. Quindi moltiplica 21,5 per 45, quindi il risultato è 967,5 metri. 967, 5 è l'entità del tuo spostamento, o quanto lontano si è spostata la tua auto dal punto di partenza.
Parte 3 di 5: quando si conoscono la velocità iniziale, l'accelerazione e il tempo
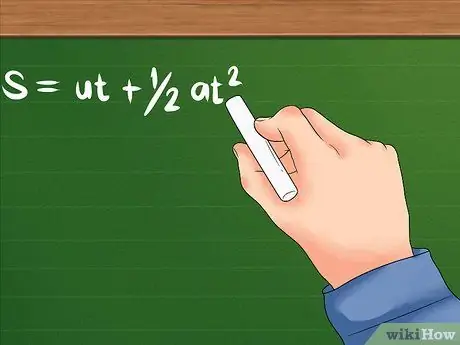
Passaggio 1. Utilizzare la formula modificata quando l'accelerazione è nota oltre alla velocità e al tempo iniziali
Alcune domande ti diranno solo quanto velocemente l'oggetto si sta muovendo all'inizio, quanto velocemente l'oggetto sta iniziando ad accelerare e quanto lontano si sta muovendo l'oggetto. Avrai bisogno della seguente formula.
- La formula per questo problema è: S = ut + 1/2at². U indica ancora la velocità iniziale; a è l'accelerazione dell'oggetto, o la velocità con cui inizia a cambiare la sua velocità. T può significare il tempo impiegato o una certa quantità di tempo impiegata da un oggetto per accelerare. Entrambi utilizzeranno unità di tempo come secondi, ore e altre.
- Supponiamo che un'auto che si muove a 25 m/s (velocità iniziale) inizi ad accelerare a 3 m/s2 (accelerazione) per 4 secondi (tempo). Qual è lo spostamento dell'auto dopo 4 secondi?

Passaggio 2. Immettere i valori nella formula
A differenza della formula precedente, qui è rappresentata solo la velocità iniziale, quindi assicurati di inserire i dati corretti.
Sulla base dei dati di esempio sopra, la tua formula sarebbe simile a questa: S = 25(4) + 1/2(3)4². È utile aggiungere parentesi intorno alla grandezza e al tempo dell'accelerazione per aiutarti a separare i numeri
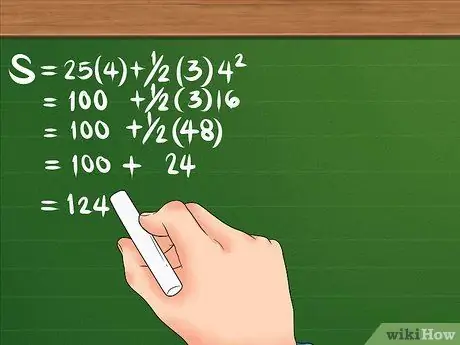
Passaggio 3. Calcola lo spostamento facendolo nell'ordine corretto delle operazioni
Un modo rapido per aiutarti a ricordare la sequenza delle operazioni è il ponte degli asini Kur ir Kua ci Kadang Ba wa Juragan Turtles. Questo rappresenta l'ordine corretto: parentesi, quadrati, moltiplicazione, divisione, addizione e sottrazione.
Esaminiamo di nuovo la formula: S = 25(4) + 1/2(3)4². Primo, quadrato 4, il risultato è 16. Quindi, moltiplica 16 per 3, ottenendo 48; poi moltiplica anche 25 per 4, per fare 100. Dividi 48 per 2, per fare 24. La tua equazione dovrebbe assomigliare a questa: S = 100 + 24. Una volta sommati i due, lo spostamento è di 124 metri
Parte 4 di 5: Calcolo dello spostamento angolare

Passaggio 1. Trova lo spostamento angolare mentre l'oggetto si muove lungo un percorso circolare
Anche se continuerai a calcolare lo spostamento utilizzando una linea retta, dovrai trovare la differenza tra le posizioni iniziale e finale dell'oggetto mentre si sposta lungo un percorso circolare.
- Immagina una ragazza seduta su una giostra. Mentre gira con la giostra, si sposterà lungo un percorso circolare. Lo spostamento angolare tenta di trovare la distanza più breve tra le posizioni iniziale e finale quando l'oggetto non si muove in linea retta.
- La formula per lo spostamento angolare è: = S/r, dove S è lo spostamento lineare, r è il raggio ed è lo spostamento angolare. Lo spostamento lineare è la distanza di spostamento di un oggetto lungo un arco. Il raggio è la distanza dell'oggetto dal centro del cerchio. Lo spostamento angolare è il valore che vogliamo trovare.

Passaggio 2. Inserisci lo spostamento lineare e il raggio nell'equazione
Ricorda che il raggio è la distanza dal centro del cerchio; alcuni problemi ti diranno il diametro di un cerchio, che deve essere diviso per 2 per trovare il raggio.
- Ecco un esempio di problema: una ragazza va su una giostra. Il sedile è a 1 metro dal centro del cerchio (il raggio). Se la ragazza si muove lungo una traiettoria ad arco di 1,5 metri (spostamento lineare), qual è il suo spostamento angolare?
- La tua equazione sarà simile a questa: = 1.5/1.
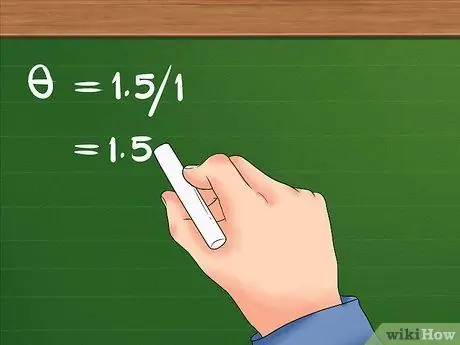
Passaggio 3. Dividere lo spostamento lineare per il raggio
Questa divisione risulterà nello spostamento angolare dell'oggetto.
- Dopo aver diviso 1,5 per 1, il risultato è 1,5. Lo spostamento angolare della ragazza è 1,5 radianti.
- Poiché lo spostamento angolare misura quanto un oggetto ruota dalla sua posizione iniziale, dovrebbe essere misurato come un angolo, non come una distanza. Il radiante è l'unità utilizzata per misurare gli angoli.
Parte 5 di 5: Comprensione della migrazione
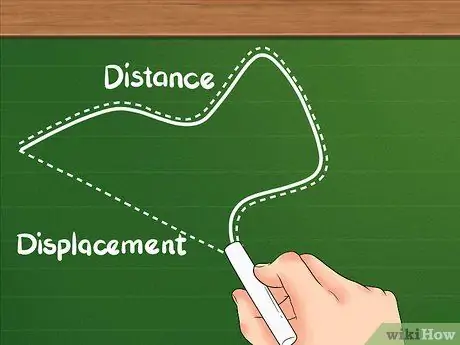
Passaggio 1. Sappi che la distanza ha una definizione diversa dallo spostamento
Distanza mostra la distanza totale percorsa dall'oggetto.
- La distanza è spesso nota come quantità scalare. Distanza mostra la distanza percorsa da un oggetto indipendentemente dalla direzione dell'oggetto.
- Ad esempio, se fai 2 passi verso est, 2 passi verso sud, 2 passi verso ovest e poi 2 passi verso nord, tornerai alla posizione di partenza. Anche se hai superato il totale distanza 10 passi di distanza, basta spostare 0 passi perché la tua posizione finale è la stessa della tua posizione di partenza (il tuo percorso assomiglia a una scatola).

Passaggio 2. Comprendere che lo spostamento è la differenza tra due posizioni
Lo spostamento non è la somma totale del movimento come la distanza; sposta l'attenzione sull'area tra le posizioni di partenza e di arrivo.
- Lo spostamento è chiamato una quantità vettoriale e mostra il cambiamento nella posizione di un oggetto considerando la direzione del movimento dell'oggetto.
- Ad esempio, cammini verso est per 5 passi. Se torni indietro di 5 passi verso ovest, ti sposterai nella direzione opposta rispetto alla tua posizione originale. Anche se hai percorso 10 passaggi, la tua posizione non è cambiata; il tuo spostamento è di 0 passi.

Passaggio 3. Ricorda le parole avanti e indietro quando cerchi di immaginare lo spostamento
Lo spostamento nella direzione opposta elimina lo spostamento di un oggetto.
Immagina un allenatore di football che fa avanti e indietro a bordo campo. Mentre urlava ai giocatori, si è spostato da sinistra a destra diverse volte. Se lo guardi mentre si sposta da sinistra a destra, osservi la distanza totale che ha percorso. Tuttavia, supponiamo che l'allenatore si fermi a parlare con il quarterback a bordo campo. Se si trova in un punto diverso dalla sua posizione iniziale prima di muoversi, allora stai osservando il movimento dell'allenatore

Passaggio 4. Sappi che lo spostamento viene misurato utilizzando un percorso rettilineo, non un percorso circolare
Per trovare lo spostamento, devi trovare il modo più breve ed efficiente per calcolare la differenza tra due punti.
- Un percorso circolare ti porterà dalla posizione di partenza alla posizione finale, ma non è il percorso più breve. Per aiutarti a visualizzarlo, immagina di camminare in linea retta e di imbatterti in un pilastro. Non puoi sfondare questo pilastro, quindi aggiralo. Anche se la tua posizione finale è la stessa di se avessi sfondato il pilastro, avrai bisogno di ulteriori passaggi per raggiungere quell'obiettivo.
- Sebbene lo spostamento rappresenti un percorso rettilineo, sappi che puoi misurare lo spostamento di un oggetto che è attualmente muoversi in un percorso circolare. Questo spostamento è chiamato spostamento angolare e può essere calcolato trovando il percorso più breve dalla posizione iniziale alla posizione finale.

Passaggio 5. Sappi che lo spostamento può essere negativo, a differenza della distanza
Se la tua posizione finale viene raggiunta spostandoti nella direzione opposta alla tua direzione iniziale, allora il tuo spostamento è negativo.
- Ad esempio, camminiamo 5 passi verso est e poi 3 passi verso ovest. Anche se calcolando ti muovi di 2 passi dalla tua posizione di partenza, il tuo spostamento è -2 perché ti stai muovendo nella direzione opposta. La tua distanza sarà sempre positiva perché non puoi contare all'indietro in passi, chilometri e così via.
- Lo spostamento negativo non significa che lo spostamento diminuisce. Negativo significa solo che la direzione è opposta.

Passaggio 6. Renditi conto che a volte distanza e spostamento possono essere la stessa cosa
Se cammini dritto per 25 passi e ti fermi, la distanza percorsa sarà uguale allo spostamento dalla tua posizione originale.
- Questo si applica solo quando ti sposti da una posizione dalla posizione di partenza in linea retta. Ad esempio, vivi a San Francisco, in California, e ottieni un nuovo lavoro a Las Vegas, in Nevada. Devi trasferirti a Las Vegas per essere vicino al tuo lavoro. Se sali su un aereo che vola dritto da San Francisco a Las Vegas, percorrerai la stessa distanza e lo stesso spostamento x.
- Tuttavia, se guidi da San Francisco a Las Vegas, percorrerai una distanza x, ma percorrerai una distanza y. Poiché la guida di un'auto di solito ha direzioni variabili (a est di questa strada, a ovest di quella strada), percorrerai distanze maggiori rispetto alla distanza più breve tra le due città.






