- Autore Jason Gerald [email protected].
- Public 2024-01-15 08:17.
- Ultima modifica 2025-01-23 12:21.
Ci sono vari modi per fare la divisione. Puoi dividere decimali, frazioni o anche esponenti e utilizzare una divisione lunga o corta. Se vuoi conoscere i diversi modi di dividere i numeri, segui i passaggi seguenti.
Fare un passo
Metodo 1 di 5: eseguire la divisione in serie lunghe

Passaggio 1. Annota le domande
Per eseguire una divisione lunga, posiziona il denominatore (il numero che dividerà) all'esterno della barra del divisore e il numeratore (il numero da dividere) all'interno della barra del divisore.
Ad esempio: 136÷3

Passaggio 2. Dividi la prima cifra del numeratore per il denominatore (se possibile)
In questo esempio, 1 non è divisibile per 3, quindi metti uno 0 sopra la barra del divisore e vai al passaggio successivo. Sottrai 1 per 0 e metti il risultato sotto il numero 1.

Passaggio 3. Dividi il numero del resto della prima cifra del numeratore e della seconda cifra del numeratore per il denominatore
Poiché 1 non può essere diviso per 3, viene ancora utilizzato il numero 1. Devi sottrarre 3. Ora, dividi 13 per 3. Poiché 3 x 4 = 12, metti il 4 sopra la barra del divisore (a destra di 0), quindi sottrai 13 per 12 e scrivi il risultato sotto di esso.

Passaggio 4. Dividi i numeri rimanenti per il denominatore
Abbassa il numero 6 a destra di 1, per ottenere 16. Ora, dividi 16 per 3. Poiché 3 x 5 = 15, scrivi il numero 5 a destra del numero 4, sottrai 16 per 15 e scrivi il risultato (16-15= 1) sotto di esso.

Passaggio 5. Scrivi il resto accanto al quoziente
La tua risposta finale è 45 con 1 rimanente o 45 R1.
Metodo 2 di 5: eseguire divisioni brevi

Passaggio 1. Annota le domande
Scrivi il denominatore (il numero da dividere) all'esterno della barra del divisore e il numeratore (il numero da dividere) all'interno della barra del divisore. Nota che nella divisione corta, il denominatore non può essere più di una cifra.
Ad esempio, 518 4

Passaggio 2. Dividi la prima cifra del numeratore per il denominatore
5 4 = 1 R1. Posiziona il quoziente (1) sopra la barra divisoria lunga. Scrivi il resto sopra la prima cifra del numeratore. Metti un piccolo 1 su 5 per ricordarti che ti rimane 1 quando dividi 5 per 4. Il 518 dovrebbe ora assomigliare a questo: 5118

Passaggio 3. Dividi il numero formato dal resto e la seconda cifra del numeratore per il denominatore
Il numero successivo è 11 che si ottiene dal valore residuo (1) e dalla seconda cifra del numeratore (1). 11 4 = 2 R 3 perché 4 x 2 = 8 con resto 3. Scrivi il valore residuo sopra la seconda cifra del numeratore. Metti 3 su 1. Il numeratore iniziale (518) ora ha questo aspetto: 51138

Passaggio 4. Dividi i numeri rimanenti per il denominatore
Il numero rimanente è 38; il numero 3 deriva dal resto della fase precedente e 8 è l'ultima cifra del numeratore. Calcola 38 4 = 9 R2. Poiché 4 x 9 = 36, scrivi "R2" sopra la barra di divisione perché 38 - 36 = 2.

Passaggio 5. Annota la risposta finale
Il risultato finale e il quoziente sono sopra la barra del divisore. La risposta è 518 4 = 129 R2.
Metodo 3 di 5: dividere le frazioni

Passaggio 1. Annota le domande
Per dividere una frazione, scrivi semplicemente la prima frazione seguita dal simbolo di divisione e poi la seconda frazione.
Ad esempio: 3/4 5/8

Passaggio 2. Invertire il numeratore e il denominatore della seconda frazione
La seconda frazione è ora reciproca.
Esempio: 3/4 8/5

Passaggio 3. Cambia il simbolo di divisione con il simbolo dei tempi
Per dividere una frazione, moltiplichi la prima frazione per il reciproco della seconda.
Esempio: 3/4 x 8/5
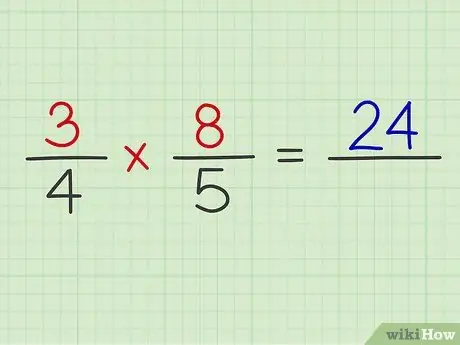
Passaggio 4. Moltiplica il numeratore di entrambe le frazioni
Fai come moltiplicare due frazioni regolari.
Esempio: 3 x 8 = 24
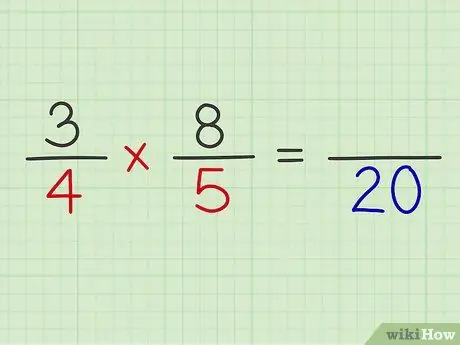
Passaggio 5. Moltiplica i denominatori di entrambe le frazioni
Completa il calcolo moltiplicando le due frazioni.
Esempio: 4 x 5 = 20
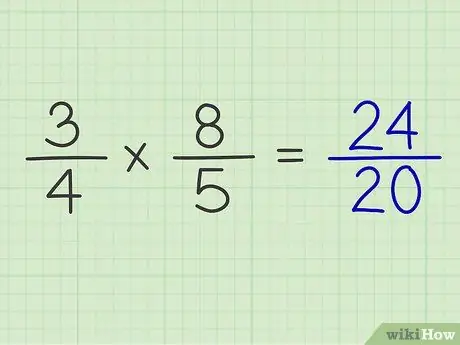
Passaggio 6. Metti il prodotto del numeratore sopra il prodotto del denominatore
Dopo aver moltiplicato il numeratore e il denominatore delle due frazioni, puoi ottenere il risultato del calcolo di entrambe le frazioni.
Esempio: 3/4 x 8/5 = 24/20

Passaggio 7. Semplifica le frazioni
Trovare il Massimo Comune Fattore, ovvero il numero più grande che divide equamente numeratore e denominatore. In questo caso, il massimo comun 24 e 20 è 4. Per dimostrarlo, scrivi tutti i numeratori e denominatori e cerchia il numero dei massimi comun di entrambi.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Poiché 4 è il massimo comun divisore di 24 e 20, basta dividere i due numeri per 4 per semplificare la frazione.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Passaggio 8. Riscrivi la frazione come numero misto (opzionale)
Il trucco, basta dividere il numeratore per il denominatore e scrivere il risultato come un numero intero. Dopodiché scrivi il resto della divisione come nuovo numeratore e il denominatore della frazione non cambia. Poiché 6 diviso 5 risulta 1 con resto 1, scrivi il numero intero 1, seguito dal nuovo numeratore 1, quindi dal denominatore 5 per ottenere un numero misto 1 1/5.
Esempio: 6/5 = 1 1/5
Metodo 4 di 5: dividere l'esponente

Passaggio 1. Assicurati che gli esponenti/potenze abbiano lo stesso numero di base
Puoi dividere gli esponenti solo se hanno lo stesso numero di base. Altrimenti, puoi provare a manipolarli finché non ottieni lo stesso numero di base.
Esempio: x8 X5

Passaggio 2. Sottrarre l'esponente
Puoi semplicemente sottrarre il primo esponente per il secondo. Non badare ai numeri di base per ora.
Esempio: 8 - 5 = 3
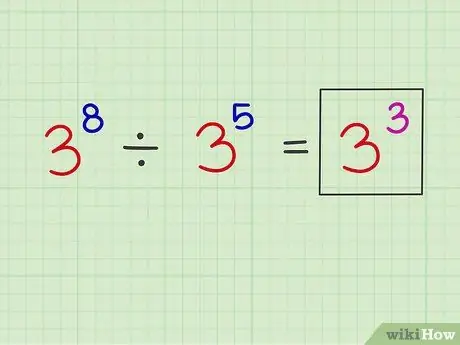
Passaggio 3. Posiziona il nuovo esponente sopra il numero di base originale
Ora puoi scrivere il nuovo esponente sul numero di base originale.
Esempio: x8 X5 = x3
Metodo 5 di 5: divisione dei numeri decimali

Passaggio 1. Annota le domande
Scrivi il denominatore (il numero da dividere) all'esterno della barra del divisore e il numeratore (il numero da dividere) all'interno della barra del divisore. Nella divisione decimale, il tuo obiettivo è convertire un numero decimale in un numero intero.
Esempio: 65.5.5

Passaggio 2. Cambia il denominatore in un numero intero
Basta far scorrere il punto decimale di una cifra a destra per cambiare 0,5 in 5, ovvero 5, 0.

Passaggio 3. Modificare il numeratore spostando la virgola dello stesso numero di cifre del denominatore
Poiché sposti il punto decimale del numeratore di una cifra a destra in modo che diventi un numero intero, anche il punto decimale del denominatore viene spostato di una cifra a destra in modo che 65,5 diventi 655.
Se sposti il punto decimale del numeratore oltre tutte le sue cifre, significa che devi aggiungere zeri alle cifre ogni volta che il punto decimale viene spostato. Ad esempio, se il punto decimale 7, 2 viene spostato di tre cifre a destra, il numero cambia in 7.200 perché lo spazio vuoto di due cifre viene riempito con zeri

Passaggio 4. Posiziona il punto decimale sulla barra di divisione lunga appena sopra il punto decimale nel numeratore
Poiché stai spostando il punto decimale di una cifra per rendere 0,5 un numero intero, è una buona idea posizionare il punto decimale sopra la barra di divisione esattamente dove viene spostato il punto decimale, cioè dopo gli ultimi 5 in 655.

Passaggio 5. Risolvi il problema con una semplice divisione lunga
Per dividere 655 per 5, i passaggi sono:
- Dividi le centinaia del numeratore (6) per il denominatore (5). Il risultato è 1 con resto 1. Scrivi il numero 1 sopra la barra del divisore e 5 sotto il numero 6 da sottrarre.
- Il resto di 1 viene sottratto dalla cifra delle decine del numeratore (5) in modo da ottenere 15. Dividi 15 per 5 per ottenere 3. Scrivi 3 sopra la barra del divisore, a destra di 1.
- Elimina le ultime 5 cifre. Dividi 5 per 5 per ottenere 1. Scrivi il numero 1 sopra la barra del divisore, a destra del numero 3. Non c'è resto perché 5 è divisibile per 5.
- La risposta della divisione sequenziale lunga è 655 5 = 131. Questo risultato è lo stesso della risposta alle domande 65,5 0,5.






