- Autore Jason Gerald [email protected].
- Public 2024-01-15 08:17.
- Ultima modifica 2025-01-23 12:21.
All'inizio, dividere una frazione per una frazione può sembrare confuso, ma in realtà è davvero facile. Tutto quello che devi fare è capovolgere, moltiplicare e semplificare! Questo articolo ti guiderà attraverso il processo e ti mostrerà quanto sia facile dividere una frazione per una frazione.
Fare un passo
Parte 1 di 2: Capire come dividere frazioni per frazioni
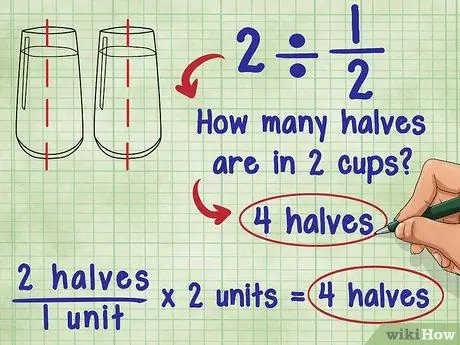
Passaggio 1. Pensa a cosa significa dividere per una frazione
Di 2 ÷ 1/2 chiese Ada: "Quante metà ci sono in 2?" La risposta è 4 perché ogni unità (1) è composta da due “metà”, e ci sono 2 unità totali: 2 “metà”/1 unità * 2 unità = 4 “metà”.
- Prova a immaginare la stessa equazione usando un bicchiere d'acqua: quanti bicchieri e mezzo d'acqua ci sono in 2 bicchieri d'acqua? Puoi versare 2 tazze e mezzo d'acqua in ogni bicchiere d'acqua. Ciò significa, in pratica, che sommi i "mezzi" bicchieri d'acqua e hai due bicchieri: 2 "metà"/1 tazza * 2 tazze = 4 "metà".
- Ciò significa che se la frazione che stai dividendo è compresa tra 0 e 1, la risposta è sempre maggiore del numero originale! Questo è vero quando dividi un numero intero o una frazione per una frazione.

Passaggio 2. Comprendi che dividere è l'opposto della moltiplicazione
Pertanto, la divisione per una frazione può essere risolta moltiplicando per il reciproco della frazione. Il reciproco di una frazione (chiamato anche “moltiplicazione inversa”) è la frazione che viene invertita, in modo che numeratore e denominatore si scambino di posto. Tra un attimo, divideremo frazioni per frazioni, trovando il reciproco della seconda frazione e moltiplicando entrambe le frazioni. Tuttavia, esaminiamo prima alcuni degli opposti:
- Il reciproco di 3/4 è 4/3.
- L'opposto di 7/5 è 5/7.
- Il reciproco di 1/2 è 2/1 o 2.
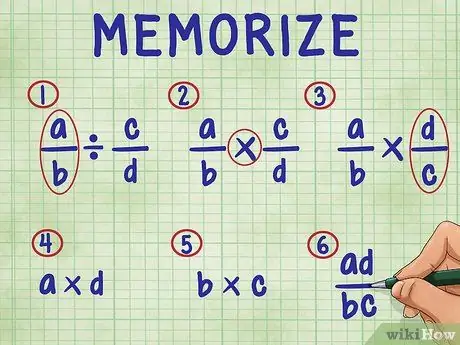
Passaggio 3. Ricorda i seguenti passaggi per dividere una frazione per una frazione
In ordine, i passaggi includono:
- Lascia la prima frazione nell'equazione.
- Cambia il segno di divisione nel segno di moltiplicazione.
- Invertire la seconda frazione (trovare il suo reciproco).
- Moltiplica il numeratore (numero superiore) di entrambe le frazioni. Il risultato della moltiplicazione è il numeratore (in alto) della tua risposta.
- Moltiplica il denominatore (numero inferiore) di entrambe le frazioni. Il prodotto del prodotto è il denominatore della tua risposta.
- Semplifica le tue frazioni semplificandole ai loro termini più semplici.
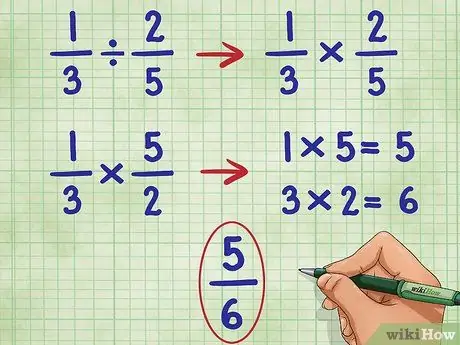
Passaggio 4. Eseguire questi passaggi per l'esempio 1/3 2/5
Inizieremo omettendo la prima frazione e convertendo il segno di divisione nel segno di moltiplicazione:
- 1/3 ÷ 2/5 = diventa:
- 1/3 * _ =
- Ora, invertiamo la seconda frazione (2/5) per trovare il suo reciproco, che è 5/2:
- 1/3 * 5/2 =
- Ora, moltiplica il numeratore (numero superiore) di entrambe le frazioni, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Ora, moltiplica il denominatore (numero inferiore) di entrambe le frazioni, 3*2 = 6.
- Ora abbiamo: 1/3 * 5/2 = 5/6
- Questa frazione non può essere ulteriormente semplificata, quindi abbiamo la nostra risposta.

Passaggio 5. Cerca di ricordare le seguenti rime per aiutarti a ricordare:
"Divisione delle frazioni è facile, invertire la seconda frazione, quindi moltiplicare. Non dimenticare di semplificare, prima che sia il momento di mangiare."
Un altro utile promemoria ti dice cosa fare con ciascuna parte dell'equazione: "Lasciami (prima frazione), Cambiami (segno di divisione), Invertimi (seconda frazione)."
Parte 2 di 2: divisione di frazioni per frazioni nei problemi
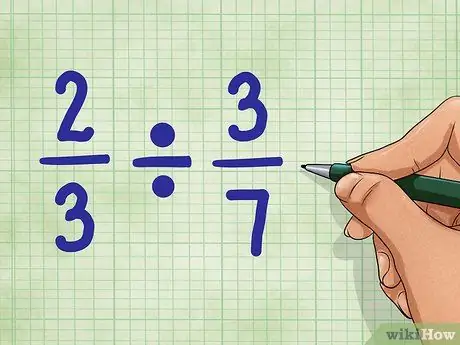
Passaggio 1. Inizia con domande di esempio
usiamo 2/3 ÷ 3/7. Questa domanda richiede il numero di parti pari a 3/7, che si trova nel valore 2/3. Non preoccuparti. Non è così difficile come sembra!
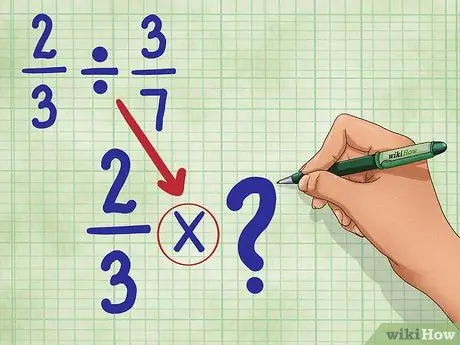
Passaggio 2. Converti il segno di divisione nel segno di moltiplicazione
La tua nuova equazione sarà: 2/3 * _ (Tra poco riempiremo questo vuoto.)
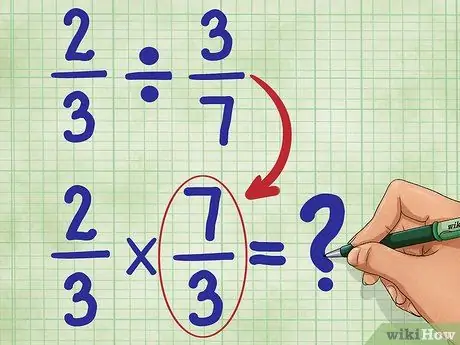
Passaggio 3. Ora trova il reciproco della seconda frazione
Ciò significa capovolgere 3/7 in modo che il numeratore (3) sia ora in basso e il denominatore (7) sia ora in alto. Il reciproco di 3/7 è 7/3. Ora scrivi la tua nuova equazione:
2/3 * 7/3 = _

Passaggio 4. Moltiplica le tue frazioni
Innanzitutto, moltiplica i numeratori di entrambe le frazioni: 2 * 7 = 14. 14 è il numeratore (numero superiore) della tua risposta. Quindi, moltiplica i denominatori di entrambe le frazioni: 3 * 3 = 9. 9 è il denominatore (numero inferiore) della tua risposta. Ora, lo sai 2/3 * 7/3 = 14/9.
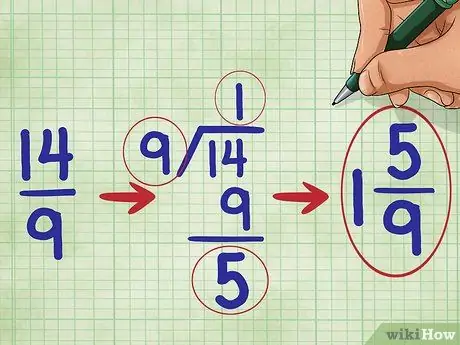
Passaggio 5. Semplifica la tua frazione
In questo problema, poiché il numeratore della frazione è maggiore del denominatore, sappiamo che la nostra frazione è maggiore di 1. Dobbiamo convertirla in un numero misto. (Un numero misto è un numero intero e una frazione combinati, ad esempio 1 2/3.))
-
Innanzitutto, dividi il numeratore
Passaggio 14. insieme a 9.
Il numero 14 diviso 9 è uguale a uno con resto 5, quindi dovresti scrivere la tua frazione semplificata come: 1 5/9 ("un cinque-nove").
- Fermati, hai trovato la risposta! Puoi specificare che non puoi più semplificare la frazione perché il denominatore non è divisibile per il numeratore (9 non è divisibile per 5) e il numeratore è un numero primo, ovvero un intero divisibile solo per uno e il numero stesso.
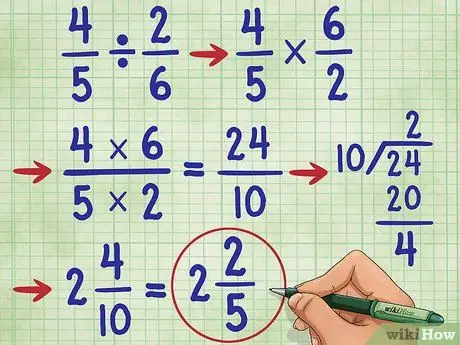
Passaggio 6. Prova un altro esempio
Proviamo la domanda 4/5 ÷ 2/6 =. Innanzitutto, cambia il segno di divisione nel segno di moltiplicazione (4/5 * _ =), quindi trova il reciproco di 2/6, che è 6/2. Ora hai l'equazione: 4/5 * 6/2 =_. Ora, moltiplica il numeratore, 4 * 6 = 24, e il denominatore 5* 2 = 10. Ora hai 4/5 * 6/2 = 24/10.
Ora, semplifica la frazione. Poiché il numeratore è maggiore del denominatore, dobbiamo convertire questa frazione in un numero misto.
- Innanzitutto, dividi il numeratore per il denominatore, (24/10 = 2 rimanenti 4).
- Scrivi la risposta come 2 4/10. Possiamo ancora semplificare di nuovo questa frazione!
- Nota che 4 e 10 sono numeri pari. Quindi, il primo passo per semplificarlo è dividere ogni numero per 2. Otteniamo 2/5.
- Poiché il denominatore (5) non è divisibile per il numeratore (2) e 5 è un numero primo, sappiamo che questa frazione non può essere ulteriormente semplificata. Quindi, la nostra risposta è: 2 2/5.

Passaggio 7. Ottieni ulteriore assistenza per semplificare le frazioni
Probabilmente hai passato molto tempo a imparare a semplificare le frazioni prima di provare a dividerle l'una per l'altra. Tuttavia, se hai bisogno di un aggiornamento o di altro aiuto, ci sono alcuni ottimi articoli online che possono esserti di grande aiuto.
Articoli correlati su wikiHow
- Conversione di frazioni comuni in decimali
- Calcolo dell'area di un cerchio
- Dividere i polinomi usando la divisione sintetica
- Divisione di frazioni miste






