Dividere frazioni per numeri interi non è così difficile come sembra. Per dividere una frazione per un intero, tutto ciò che devi fare è convertire l'intero numero in una frazione, trovare il reciproco della frazione e moltiplicare il risultato per la prima frazione. Se vuoi sapere come farlo, segui questi passaggi:
Fare un passo
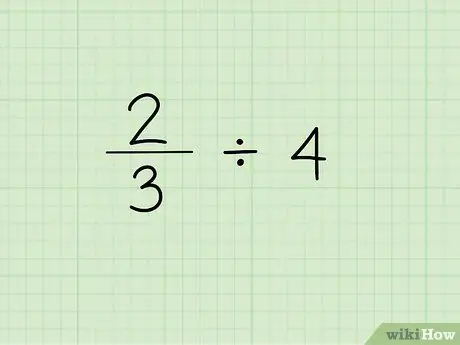
Passaggio 1. Annotare il problema
Il primo passo per dividere una frazione per un intero è scrivere la frazione seguita dal segno di divisione e dall'intero necessario per dividere la frazione. Diciamo che stiamo lavorando con il seguente problema: 2/3 4.
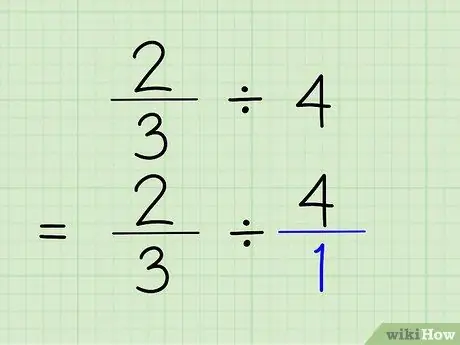
Passaggio 2. Converti interi in frazioni
Per convertire un intero in una frazione, tutto ciò che devi fare è posizionare l'intero sopra il numero 1. L'intero diventa il numeratore e 1 diventa il denominatore della frazione. Dire 4/1 è davvero come dire 4, perché stai solo mostrando che il numero contiene "1" 4 volte. Il problema sarà 2/3 4/1.
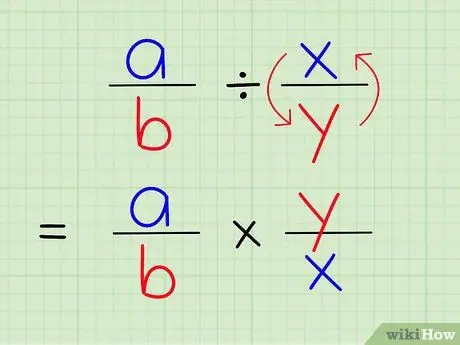
Passaggio 3. Dividere una frazione per un'altra equivale a moltiplicare quella frazione per il reciproco di un'altra frazione
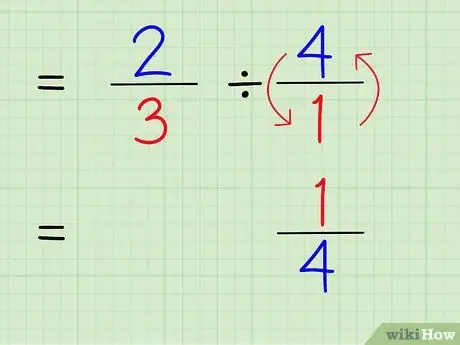
Passaggio 4. Scrivi il reciproco dell'intero
Per trovare il reciproco di un numero, scambiare numeratore e denominatore del numero. Pertanto, per trovare il reciproco di 4/1, scambia semplicemente numeratore e denominatore in modo che il numero diventi 1/4.
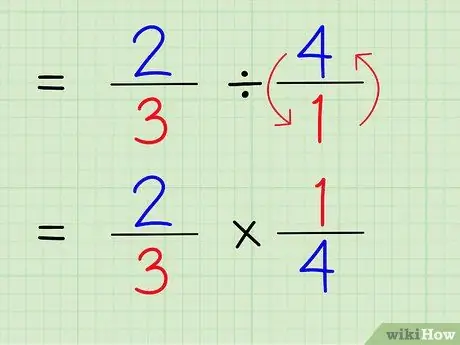
Passaggio 5. Cambia il segno di divisione nel segno di moltiplicazione
Il problema sarà 2/3 x 1/4.
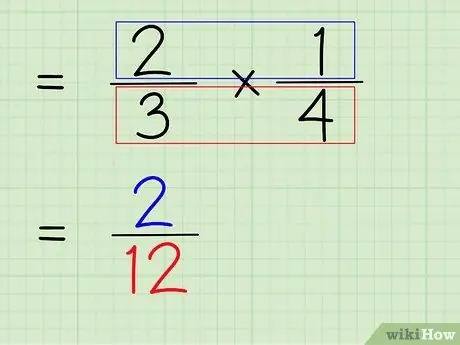
Passaggio 6. Moltiplica il numeratore e il denominatore della frazione
Quindi, il passo successivo è moltiplicare il numeratore e il denominatore della frazione per ottenere un nuovo numeratore e denominatore come risposta finale.
- Per moltiplicare i numeratori, basta moltiplicare 2 x 1 per ottenere 2.
- Per moltiplicare i denominatori, basta moltiplicare 3 x 4 per ottenere 12.
- 2/3 x 1/4 = 2/12
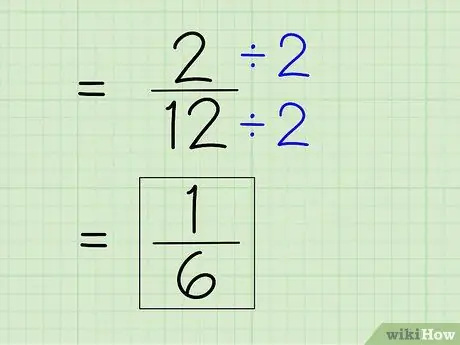
Passaggio 7. Semplifica la frazione
Per semplificare una frazione, devi trovare il denominatore più piccolo, il che significa che devi dividere numeratore e denominatore per qualsiasi numero che divide entrambi i numeri. Poiché 2 è il numeratore, dovrai vedere se 2 può dividere completamente 12 -- può farlo perché 12 è un numero pari. Quindi, dividi il numeratore e il denominatore per 2 per ottenere un nuovo numeratore e denominatore per ottenere una risposta semplice.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- La frazione 2/12 può essere semplificata a 1/6. Questa è la tua risposta finale.
Suggerimenti
- Questo serve per aiutare la memoria, un modo semplice per ricordare come fare tutti questi calcoli. Tieni a mente: "È facile dividere le frazioni, invertire il secondo numero e moltiplicare!"
- Un'altra variazione del metodo di cui sopra è JGB/JBG. Non modificare il primo numero. Passa alla moltiplicazione. Inverti l'ultimo numero. Oppure prima B poi G.
- Se annulli il calcolo prima di moltiplicarlo, potresti non aver bisogno di trovare la forma più semplice della frazione perché il risultato è già nella forma più semplice della frazione come puoi vedere. Nel nostro esempio, prima di moltiplicare 2/3 × 1/4, possiamo vedere che il primo numeratore (2) e il secondo denominatore (4) hanno lo stesso moltiplicatore di 2, che possiamo cancellare prima di continuare il calcolo. Questo converte il problema in 1/3 × 1/2, che dà un risultato immediato 1/6 e ci fa risparmiare tempo semplificando la frazione in una fase successiva.
- Se una delle tue frazioni è negativa, questo metodo è ancora praticabile; assicurati di tenere traccia dei segnali mentre esegui questi passaggi.
