- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:17.
- Ultima modifica 2025-06-01 06:06.
Il valore P è una misurazione statistica che aiuta gli scienziati a determinare se la loro ipotesi è corretta. Il valore P viene utilizzato per determinare se i risultati del loro esperimento rientrano nell'intervallo di valori normali per le cose studiate. Di solito, se il valore P di un set di dati scende al di sotto di un certo valore predeterminato (ad esempio, 0,05), gli scienziati rifiuteranno l'ipotesi nulla del loro esperimento - in altre parole, escluderanno un'ipotesi in cui la variabile sperimentale ha nessun effetto significativo sul risultato. Oggi, i valori di p si trovano solitamente nelle tabelle di riferimento calcolando il valore del chi quadrato.
Fare un passo

Passaggio 1. Determinare i risultati attesi dell'esperimento
Di solito, quando gli scienziati conducono un esperimento ed esaminano i risultati, hanno già un'idea dei risultati normali o ordinari in anticipo. Questo può essere basato sui risultati di esperimenti precedenti, serie di dati osservativi affidabili, letteratura scientifica e/o altre fonti. Per il tuo esperimento, determina il risultato atteso e scrivilo come un numero.
Esempio: supponiamo che uno studio precedente abbia mostrato che, a livello nazionale, i biglietti per eccesso di velocità sono stati emessi più spesso per le auto rosse che per le auto blu. Supponiamo che il risultato medio a livello nazionale mostri un rapporto di 2:1 con il rapporto delle auto rosse maggiore. Vogliamo scoprire se anche la polizia della nostra città ha la stessa tendenza analizzando la multa per eccesso di velocità emessa dalla polizia della nostra città. Se prendessimo un campione casuale di 150 multe per eccesso di velocità date alle auto rosse e blu nella nostra città, ci aspetteremmo 100 per macchina rossa e 50 per le auto blu se la Questura della nostra città rilascia una multa secondo il confronto a livello nazionale.

Passaggio 2. Determina le tue osservazioni sperimentali
Ora che hai determinato il valore previsto, puoi eseguire l'esperimento e trovare il valore (o osservazione) vero. Ancora una volta, scrivi il risultato come un numero. Se manipoliamo alcune condizioni sperimentali e i risultati osservati differiscono dai risultati attesi, esistono due possibilità: o è successo per caso, oppure è stata la nostra manipolazione delle variabili sperimentali a causare questa differenza. Lo scopo di trovare il p-value è fondamentalmente determinare se i risultati osservati differiscono dai risultati attesi fino a un punto in cui l'ipotesi nulla - l'ipotesi che non vi sia alcuna relazione tra la variabile sperimentale e i risultati osservati - non può essere rifiutata.
Esempio: supponiamo, nella nostra città, di selezionare a caso 150 multe per eccesso di velocità che vengono assegnate alle auto rosse e blu. Noi abbiamo 90 un biglietto per una macchina rossa e 60 per l'auto blu. Questo è diverso dal risultato che ci aspettavamo, cioè 100 e 50. La nostra manipolazione sperimentale (in questo caso, cambiando la fonte dei dati da nazionale a locale) ha causato qualche cambiamento nei risultati, o la nostra polizia cittadina ha avuto le stesse tendenze del livello nazionale, e abbiamo appena osservato una coincidenza? Il valore p ci aiuterà a determinarlo.

Passaggio 3. Determina i gradi di libertà per il tuo esperimento
I gradi di libertà sono una misura della quantità di variabilità nello studio, che è determinata dal numero di categorie esaminate. L'equazione per i gradi di libertà è Gradi di libertà = n-1, dove n è il numero di categorie o variabili analizzate nell'esperimento.
-
Esempio: il nostro esperimento ha due categorie di risultati: una per l'auto rossa e una per l'auto blu. Quindi, nel nostro esperimento, abbiamo 2-1 = 1 grado di libertà.
Se confrontiamo le auto rosse, blu e verdi, avremo
Passo 2. gradi di libertà e così via.

Passaggio 4. Confronta i risultati attesi con i risultati osservati utilizzando il chi quadrato
Chi al quadrato (scritto x2) è un valore numerico che misura la differenza tra i valori previsti e osservati dall'esperimento. L'equazione del chi quadrato è: X2 = ((o-e)2/e), dove o è il valore osservato ed e è il valore atteso. Somma i risultati di questa equazione per tutti i possibili risultati (vedi sotto).
- Nota che questa equazione usa l'operatore (sigma). In altre parole, devi calcolare ((|o-e|-.05)2/e) per ogni possibile risultato, quindi sommare i risultati per ottenere il valore del chi quadrato. Nel nostro esempio, abbiamo due risultati: un'auto che ottiene un biglietto rosso o blu. Quindi, possiamo calcolare ((o-e)2/e) due volte: una volta per l'auto rossa e una volta per l'auto blu.
-
Esempio: inseriamo i nostri valori attesi e osservazioni nell'equazione x2 = ((o-e)2/e). Ricorda che, a causa dell'operatore sigma, dobbiamo calcolare ((o-e)2/e) due volte: una volta per l'auto rossa e una volta per l'auto blu. Le fasi di lavorazione sono le seguenti:
- X2 = ((90-100)2/100) + (60-50)2/50)
- X2 = ((-10)2/100) + (10)2/50)
- X2 = (100/100) + (100/50) = 1 + 2 = 3.

Passaggio 5. Scegli un livello di significatività
Ora che conosciamo i gradi di libertà del nostro kit sperimentale e il valore chi quadrato, c'è solo un'ultima cosa che dobbiamo fare prima di poter trovare il nostro valore p: dobbiamo determinare il livello di significatività. Fondamentalmente, il livello di significatività è una misura di quanto siamo sicuri dei nostri risultati: un basso livello di significatività corrisponde a una bassa probabilità che il risultato di un esperimento sia dovuto al caso e viceversa. Il livello di significatività è scritto come decimale (es. 0,01), che corrisponde alla probabilità percentuale che l'esito dell'esperimento sia dovuto al caso (in questo caso, 1%).
- Per convenzione, gli scienziati di solito fissano un valore di significatività per i loro esperimenti allo 0,05 o al 5%. Ciò significa che i risultati sperimentali che corrispondono a questo livello di significatività hanno, al massimo, una probabilità di coincidenza del 5%. In altre parole, c'è una probabilità del 95% che i risultati siano dovuti alla manipolazione delle variabili sperimentali da parte dello scienziato, e non al caso. Per la maggior parte degli esperimenti, si ritiene che la confidenza del 95% sulla relazione tra le due variabili abbia avuto successo nel dimostrare la relazione tra le due.
- Esempio: per il nostro esempio di auto rossa e blu, seguiamo l'accordo scientifico e determiniamo il nostro livello di significatività di 0, 05.
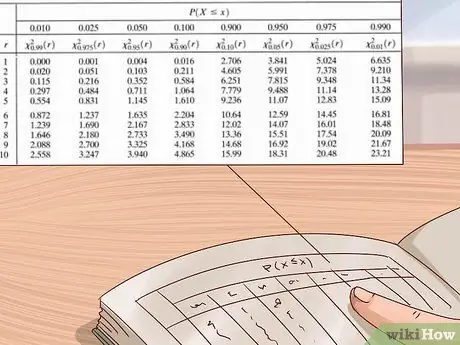
Passaggio 6. Utilizza la tabella di distribuzione del chi quadrato per stimare il tuo p-value
Scienziati e statistici utilizzano grandi tabelle di valori per calcolare i valori p per i loro esperimenti. Questa tabella è solitamente scritta con l'asse verticale a sinistra che mostra i gradi di libertà e l'asse orizzontale in alto che mostra i p-value. Usa questa tabella trovando prima i tuoi gradi di libertà, quindi leggendo le righe da sinistra a destra fino a trovare il primo valore che è maggiore del tuo valore chi quadrato. Guarda il valore p nella parte superiore della colonna: il tuo valore p è compreso tra questo valore e il valore successivo più grande (il valore giusto è a sinistra di esso).
- Le tabelle di distribuzione del chi quadrato sono disponibili da una varietà di fonti: possono essere facilmente trovate online o nei libri di testo di scienza o statistica. Se non ne hai uno, usa la tabella mostrata nella foto sopra o una tabella online gratuita, come quella fornita da medcalc.org qui.
-
Esempio: il nostro chi quadrato è 3. Quindi usiamo la tabella di distribuzione del chi quadrato nella foto sopra per trovare un valore p approssimativo. Poiché sappiamo che il nostro esperimento ha solo
Passo 1. gradi di libertà, inizieremo dal tavolo in alto. Andiamo da sinistra a destra in questa riga finché non troviamo un valore maggiore di
Passaggio 3. - il nostro valore chi quadrato. Il primo valore che troviamo è 3,84. Guardando questa colonna, vediamo che il valore p corrispondente è 0,05. Ciò significa che il nostro valore p è tra 0.05 e 0.1 (il prossimo valore p più grande nella tabella).

Passaggio 7. Decidi se rifiutare o difendere la tua ipotesi nulla
Poiché hai trovato un valore p approssimativo per il tuo esperimento, puoi decidere se rifiutare o meno l'ipotesi nulla dell'esperimento (come promemoria, questa è l'ipotesi che la variabile sperimentale che hai manipolato non ha avuto effetto sui risultati che hai osservato). Se il tuo p-value è inferiore al tuo valore di significatività, congratulazioni: hai dimostrato che esiste un'alta probabilità che ci sia una relazione tra le variabili che hai manipolato e le tue osservazioni. Se il tuo p-value è maggiore del tuo valore di significatività, non puoi dire con certezza che i risultati che stai osservando sono il risultato di una semplice coincidenza o manipolazione del tuo esperimento.
- Esempio: il nostro valore p è compreso tra 0,05 e 0,1, ovvero non è affatto inferiore a 0,05, quindi, sfortunatamente, non possiamo rifiutare la nostra ipotesi nulla. Ciò significa che non raggiungiamo il limite minimo di confidenza del 95% che ci siamo prefissati per cui si può dire che la polizia della nostra città emette biglietti per le auto rosse e blu in un rapporto molto diverso dalla media nazionale.
- In altre parole, c'è una probabilità del 5-10% che le nostre osservazioni non siano il risultato di un cambiamento di posizione (analizzando la nostra città, e non l'intera parte), ma siano coincidenze. Poiché stiamo cercando una probabilità inferiore al 5%, non possiamo dire che noi convinto che la polizia nella nostra città tende a multare le auto rosse - c'è una leggera ma statisticamente molto diversa possibilità che non abbiano questa tendenza.
Suggerimenti
- Una calcolatrice scientifica renderà i calcoli molto più semplici. Puoi anche cercare calcolatrici online.
- È possibile calcolare i valori p utilizzando diversi programmi per computer, inclusi software per fogli di calcolo comunemente usati e software statistici più specializzati.






