Il reciproco o reciproco è molto utile in tutti i tipi di equazioni algebriche. Ad esempio, quando dividi una frazione per un'altra, moltiplichi la prima frazione per il reciproco della seconda. È inoltre necessario utilizzare l'inverso quando si cerca l'equazione di una retta.
Fare un passo
Metodo 1 di 3: trovare l'inverso di una frazione o di un numero intero
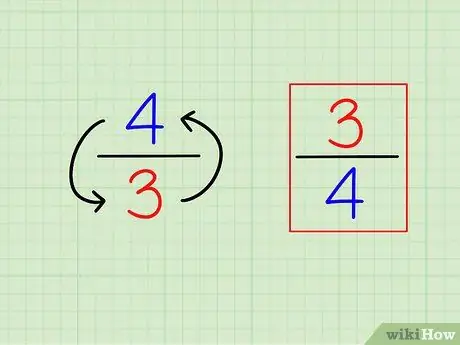
Passaggio 1. Trova il reciproco della frazione invertendo
La definizione di “reciproco” o il contrario è molto semplice. Per trovare il reciproco di qualsiasi numero intero, calcola semplicemente "1 (quel numero)". Per le frazioni, il reciproco è una frazione diversa, ovvero i numeri sono "invertiti" (inversi).
- Ad esempio, il contrario di 3/4 è 4/3.
- Qualsiasi numero moltiplicato per i suoi reciproci restituisce 1.
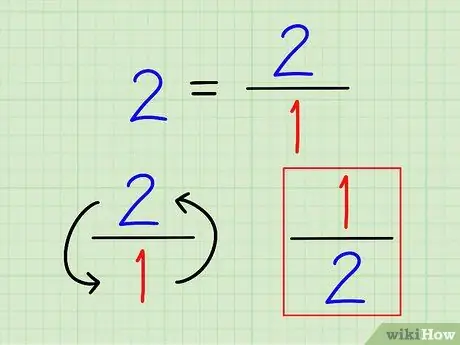
Passaggio 2. Scrivi il reciproco del numero intero come frazione
Di nuovo, il reciproco di un numero è sempre 1 (quel numero). Per i numeri interi, scrivili come frazioni. Non ha senso calcolare quel numero con un decimale.
Ad esempio, il reciproco di 2 è 1 2 = 1/2.
Metodo 2 di 3: trovare l'inverso di una frazione mista
Passaggio 1. Identificare i numeri misti
Le frazioni miste sono costituite da numeri interi e frazioni, come 24/5. Ci sono due passaggi per trovare il reciproco di un numero misto come descritto di seguito.
Passaggio 2. Converti i numeri misti in frazioni improprie
Ricorda che 1 può sempre essere scritto come (numero)/(stesso numero) e le frazioni con lo stesso denominatore (numero inferiore) possono essere sommate. Ecco un esempio usando 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
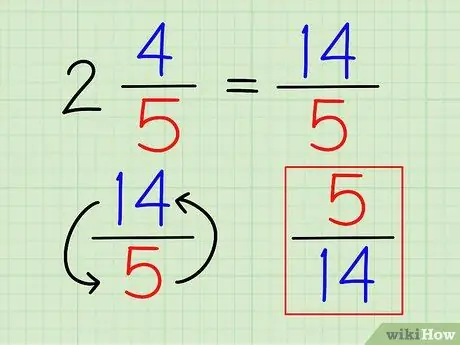
Passaggio 3. Capovolgi la frazione
Una volta che il numero è stato scritto completamente come frazione, puoi trovare il suo reciproco proprio come faresti con qualsiasi altra frazione, invertendo la frazione.
Nell'esempio sopra, il reciproco di 14/5 è 5/14.
Metodo 3 di 3: trovare l'opposto di un decimale
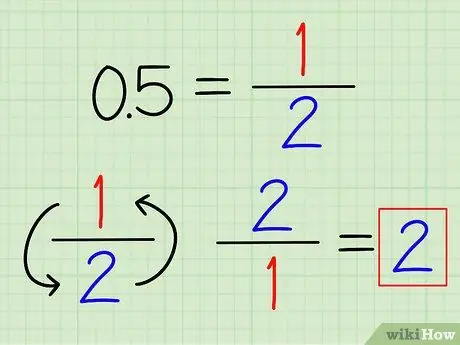
Passaggio 1. Converti i decimali in frazioni, se possibile
Potresti riconoscere alcuni numeri decimali usati di frequente, che possono essere facilmente convertiti in frazioni. Ad esempio, 0,5 = 1/2 e 0,25 = 1/4. Una volta che il decimale è stato convertito in frazione, capovolgi semplicemente la frazione per trovare il suo reciproco.
Ad esempio, il reciproco di 0,5 è 2/1 = 2.
Passaggio 2. Scrivi un problema di divisione
Se non puoi convertirlo in una frazione, calcola il reciproco del numero sotto forma di problema di divisione: 1 (decimale). Puoi usare una calcolatrice per risolverlo o procedere al passaggio successivo per risolverlo manualmente.
Ad esempio, puoi trovare il reciproco di 0,4 calcolando 1 0,4
Passaggio 3. Modificare il problema della divisione per utilizzare numeri interi
Il primo passo per dividere i decimali è spostare la virgola finché tutti i numeri non sono interi. Se sposti la virgola di entrambi i numeri dello stesso numero di passi, otterrai la risposta corretta.
Ad esempio, puoi usare 1 0, 4 e riscriverlo come 10 4. In questo caso, sposti tutte le posizioni decimali di un passo a destra, allo stesso modo in cui moltiplichi ogni numero per dieci
Passaggio 4. Risolvi il problema utilizzando la divisione lunga
Utilizzare il metodo della divisione lunga per calcolare il reciproco. Se conti 10 4, otterrai la risposta 2, 5 che è il reciproco di 0, 4.
Suggerimenti
- Il reciproco negativo di un numero è uguale al reciproco regolare, in quanto è moltiplicato per uno negativo. Ad esempio, il reciproco negativo di 3/4 è -4/3.
- Il reciproco o reciproco viene spesso definito "inverso della moltiplicazione".
- Il numero 1 è l'opposto di se stesso perché 1 1 = 1.
- Il numero 0 non ha reciproco perché 0 non è definito.
