- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:19.
- Ultima modifica 2025-06-01 06:06.
Il sistema numerico decimale (in base dieci) ha dieci possibili valori (0, 1, 2, 3, 4, 5, 6, 7, 8 o 9) per ogni posizione del numero. Al contrario, il sistema numerico binario (base due) ha solo due possibili valori rappresentati da 0 e 1 per ogni posizione numerica. Poiché il sistema numerico binario è il linguaggio interno dei computer elettronici, i programmatori di computer seri sanno come convertire dal sistema numerico decimale a quello binario. Segui questi semplici passaggi e anche come padroneggiare questa conversione.
Fare un passo
Metodo 1 di 2: divisione corta per due con resto

Passaggio 1. Determinare il problema
Per questo esempio, convertiamo il numero decimale 15610 essere un numero binario. Scrivi il numero decimale come il numero da dividere nel simbolo di divisione invertita. Scrivi la base del sistema numerico di destinazione (in questo esempio "2" per binario) come divisore fuori curva del simbolo di divisione.
- Questo metodo è molto più facile da capire quando viene disegnato su carta e molto più facile per i principianti, perché divide solo per due.
- Per evitare confusione prima e dopo la conversione, annota il numero base del sistema di numerazione che stai calcolando come pedice (lettere minuscole scritte sotto le lettere normali come segno distintivo) per ogni numero. In questo esempio, il numero decimale avrà un pedice di 10 e il numero binario avrà un pedice di 2.

Passaggio 2. Eseguire la divisione
Scrivi la risposta intera (quoziente) sotto il simbolo della divisione lunga e scrivi il resto (0 o 1) a destra del numero diviso.
Perché dividiamo per due, quando il numero da dividere è un numero pari, il resto è 0, e quando il numero da dividere è un numero dispari, il resto è 1

Passaggio 3. Continua a dividere fino a raggiungere lo zero
Continua in discesa, dividendo ogni nuovo quoziente per due e scrivendo il resto a destra di ogni numero diviso. Fermati quando il quoziente è zero.

Passaggio 4. Annotare il nuovo numero binario
A partire dal numero rimanente più basso, leggi l'ordine del resto in ordine crescente verso l'alto. In questo esempio, dovresti ottenere il risultato 10011100. Questo è l'equivalente binario del numero decimale 156. Oppure, se scritto con la sua base numerica pedice: 15610 = 100111002.
Questo metodo può essere modificato per convertire da base decimale a qualsiasi base numerica. Il divisore è 2 perché la base del sistema di numerazione di destinazione è la base 2 (binaria). Se la base del sistema di numerazione di destinazione è un'altra base, sostituire il numero di base 2 in questo metodo con il numero di base appropriato. Ad esempio, se la base di destinazione è la base 9, sostituire il numero della base 2 con 9. Il risultato finale sarà direttamente nella forma del numero della base di destinazione
Metodo 2 di 2: derivare il potere del due e la sottrazione

Passaggio 1. Inizia creando una tabella
Annota le potenze dei due numeri di base nella "base della tabella 2" da destra a sinistra. Inizia da 20, scrivilo come "1". Aumenta il grado di 1 per ogni grado. Completa la tabella finché non ottieni un numero più vicino al numero del sistema di numeri decimali che stai calcolando. Per questo esempio, convertiamo il numero decimale 15610 essere un numero binario.

Passaggio 2. Trova il numero con la maggiore potenza del numero base 2
Scegli dalla tabella il numero più grande uguale o inferiore al numero da convertire. Il numero 128 è il numero con la maggiore potenza del numero base 2 ed è anche minore di 156, quindi scrivi un numero "1" sotto questa casella nella tabella, dove il numero più grande della tabella è a sinistra (vedi tabella nell'immagine sopra). Quindi sottrai 128 dal numero iniziale, otterrai: 156 - 128 = 28.
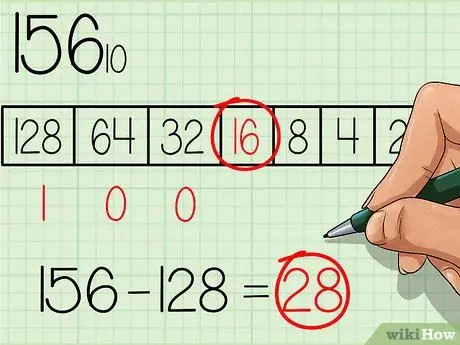
Passaggio 3. Passare alla successiva potenza più piccola nella tabella
Usando il nuovo numero (28), continua attraverso la tabella da sinistra a destra controllando se i numeri sono uguali o inferiori al nuovo numero. Il numero 64 non è inferiore a 28, quindi scrivi il numero "0" sotto la casella del numero 64. Continua finché non trovi un numero uguale o inferiore a 28.
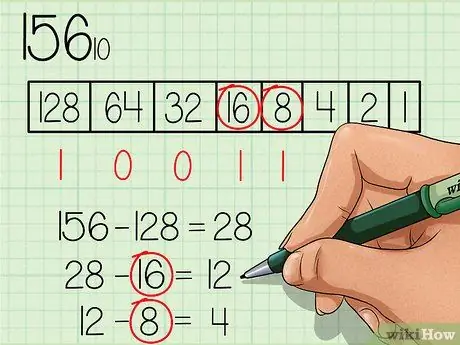
Passaggio 4. Sottrarre continuamente ogni numero uguale o inferiore al nuovo numero e contrassegnare il numero "1" sotto la casella per il numero appropriato
Il numero 16 è inferiore a 28, quindi scrivi il numero "1" sotto la casella del numero 16 e sottrai 16 da 28, in modo da ottenere un nuovo numero 12. Il numero 8 è inferiore a 12, quindi scrivi il numero "1" sotto la casella del numero 8 e sottrarre 8 da 12 per ottenere il nuovo numero 4.

Passaggio 5. Continua fino a raggiungere la fine della tabella
Ricorda di contrassegnare un "1" sotto ogni casella per i numeri uguali o inferiori al nuovo numero e uno "0" sotto ogni casella per i numeri che sono ancora maggiori del nuovo numero.
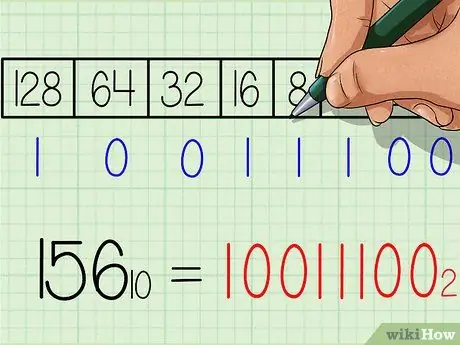
Passaggio 6. Annotare la risposta per il numero binario
Il numero sarà esattamente lo stesso da sinistra a destra della riga di numeri "1" e "0" in fondo alla tabella. Dovresti ottenere il risultato 10011100. Questo è l'equivalente binario del numero decimale 156. O se scritto con un pedice: 15610 = 100111002.
Ripetere questo metodo può aiutarti a ricordare i poteri della base due, così puoi saltare il passaggio 1
Suggerimenti
- Il programma Calcolatrice integrato nel sistema operativo può eseguire questa conversione per te, ma come programmatore è meglio iniziare con una buona comprensione di come funzionano le conversioni. Le opzioni di conversione nel programma Calcolatrice possono essere rese visibili aprendo il menu "Visualizza" e selezionando "Programmatore" (per Windows 7 e 8).
- La conversione nella direzione opposta, cioè dal sistema binario a quello decimale, di solito è più facile da imparare prima.
- Esercitati spesso a convertire i numeri decimali in binari per diventare più esperto.






