- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Ultima modifica 2025-06-01 06:06.
La matematica è difficile. È facile dimenticare anche i concetti di base quando si tenta di ricordare i molti principi e metodi diversi. Ecco due nuovi modi per semplificare le frazioni.
Fare un passo
Metodo 1 di 4: utilizzo del massimo fattore comune

Passaggio 1. Annotare i fattori numeratore e denominatore
I fattori sono numeri che puoi moltiplicare per ottenere un altro numero. Ad esempio, 3 e 4 sono fattori di 12 perché puoi moltiplicarli insieme per ottenere 12. Per scrivere i fattori di un numero, devi solo scrivere tutti i numeri che possono essere moltiplicati per ottenere quel numero e sono divisibili dai fattori.
-
Annota i fattori del numero dal più piccolo al più grande, senza dimenticare di includere il fattore 1. Ad esempio, ecco come scrivi il numeratore e il denominatore della frazione 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Passaggio 2. Trova il massimo comun divisore (GCF) del numeratore e del denominatore
GCF è il numero più grande che può dividere equamente due o più numeri. Dopo aver annotato tutti i fattori del numero, tutto ciò che devi fare è trovare il numero più grande uguale in entrambi gli elenchi di fattori.
-
24: 1, 2, 3, 4, 6,
Passaggio 8., 12, 24.
-
32: 1, 2, 4,
Passaggio 8., 16, 32.
-
Il GCF di 24 e 32 è 8 perché 8 è il numero più grande che può dividere equamente 24 e 32.

Passaggio 3. Dividi il numeratore e la frazione per il GCF
Ora che hai il GCF, tutto ciò che devi fare è dividere il numeratore e il denominatore per quel numero per semplificare la tua frazione nella sua forma più semplice. Ecco come farlo:
- 24/8 = 3
- 32/8 = 4
- La frazione semplice è 3/4.

Passaggio 4. Controlla il tuo lavoro
Se vuoi assicurarti di aver semplificato correttamente la frazione, devi solo moltiplicare il nuovo numeratore e denominatore per il loro GCF per recuperare la frazione originale. Ecco come farlo:
- 3 * 8 = 24
- 4 * 8 = 32
-
Sei tornato alla sua forma originale, che è 24/32.
Puoi anche controllare la frazione per assicurarti che non possa essere ulteriormente semplificata. Poiché 3 è un numero primo, può essere diviso solo per 1 e se stesso, e quattro non è divisibile per 3, quindi la frazione non può essere ulteriormente semplificata
Metodo 2 di 4: Continua a dividere per numeri piccoli

Passaggio 1. Scegli un numero piccolo
Usando questo metodo, devi solo scegliere un piccolo numero, come 2, 3, 4, 5 o 7, per cominciare. Guarda le frazioni per assicurarti che ogni parte sia divisibile per il numero che hai scelto. Ad esempio, se hai una frazione 24/108, non scegliere 5 perché non sono divisibili per 5. Tuttavia, se hai una frazione 25/60, 5 è il numero giusto da usare.
Per la frazione 24/32, 2 è un buon numero. Poiché entrambi i numeri sono pari, sono divisibili per 2

Passaggio 2. Dividi il numeratore e il denominatore della frazione per il numero
La nuova frazione consisterà in un nuovo numeratore e denominatore, che si ottiene dividendo la parte superiore e inferiore della frazione 24/32 per 2. Ecco come fare:
- 24/2 = 12
- 32/2 = 16
- La tua nuova frazione è 12/16.
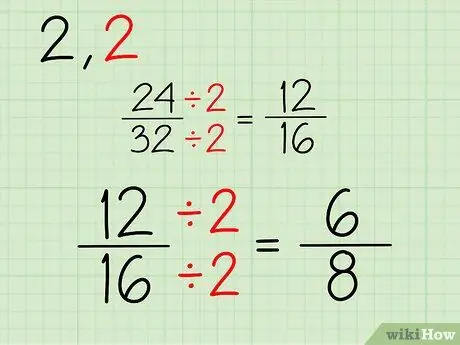
Passaggio 3. Ripetere
Continua questo processo. Poiché entrambi i numeri sono pari, puoi continuare a dividere per 2. Se uno o entrambi i numeratori e i denominatori sono numeri dispari, puoi provare a dividere per un altro numero. Ecco il processo per semplificare la frazione 12/16:
- 12/2 = 6
- 16/2 = 8
- La tua nuova frazione è 6/8.

Passaggio 4. Continua a dividere il numero finché non è più divisibile
Anche il nuovo numeratore e denominatore sono numeri pari, quindi puoi continuare a dividere per 2. Ecco come si fa:
- 6/2 = 3
- 8/2 = 4
- La tua nuova frazione è 3/4.

Passaggio 5. Assicurati che la frazione non possa essere ulteriormente semplificata
Nella frazione 3/4, 3 è un numero primo, quindi i fattori sono solo 1 e se stesso, e 4 non è divisibile per 3, quindi la frazione non può essere ulteriormente semplificata. Se il numeratore o il denominatore della frazione non può più essere diviso per il numero selezionato, potresti comunque essere in grado di dividerlo per un altro numero.
Ad esempio, se hai la frazione 10/40 e dividi numeratore e denominatore per 5, il risultato è 2/8. Non puoi continuare a dividere numeratore e frazione per 5, ma puoi dividere entrambi per 2 in modo che il risultato finale sia 1/4

Passaggio 6. Controlla il tuo lavoro
Moltiplica ancora 3/4 per 2/2 tre volte, per assicurarti di ottenere la frazione iniziale, che è 24/32. Ecco come farlo:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Nota che stai dividendo 24/32 per 2 * 2 * 2, che equivale a dividere per 8, il GCF più grande di 24 e 32.
Metodo 3 di 4: Scrivere i fattori

Passaggio 1. Scrivi la tua frazione
Lascia un ampio spazio sul lato destro del foglio: ti servirà per annotare i fattori.

Passaggio 2. Annota i fattori del numeratore e del denominatore
Solo i fattori dei due. Il modo più semplice è scrivere i fattori uno sopra l'altro. Inizia con il numero 1 e annota i fattori.
-
Ad esempio, se la tua frazione è 24/60, inizia con 24.
Annotare: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
Poi, il numero 60.
Annotare: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Passaggio 3. Trova e dividi per il massimo comun divisore
Questo termine può essere scritto come GCF nel tuo libro stampato. Qual è il numero più grande che può dividere numeratore e denominatore? Qualunque sia il numero, dividi entrambi i numeri per quel numero.
Per il nostro esempio, il numero più grande che è un fattore di entrambi i numeri è 12. Quindi, dividiamo 24 per 12 e 60 per 12, ottenendo 2/5: la nostra semplice frazione
Metodo 4 di 4: utilizzo di un albero dei fattori primi

Passaggio 1. Trova i fattori primi del numeratore e del denominatore
Un numero primo è un numero che non può essere diviso per nessun altro numero (a parte se stesso e 1, ovviamente). 2, 3, 5, 7 e 11 sono esempi di numeri primi.
- Inizia dal numeratore. Da 24, diviso in 2 e 12. Poiché 2 è già un numero primo, non è più necessario dividerlo! Quindi dividi 12 in 2 numeri: 2 e 6. 2 sono numeri primi - fantastico! Ora dividi 6 in 2 numeri: 2 e 3. Ora hai 2, 2, 2 e 3 come numeri primi.
- Ora lavora sul denominatore. Da 60, dividi il tuo albero in 2 e 30. 30 poi dividi in 2 e 15. Quindi dividi 15 in 3 e 5, entrambi numeri primi. Ora hai 2, 2, 3 e 5 come numeri primi.
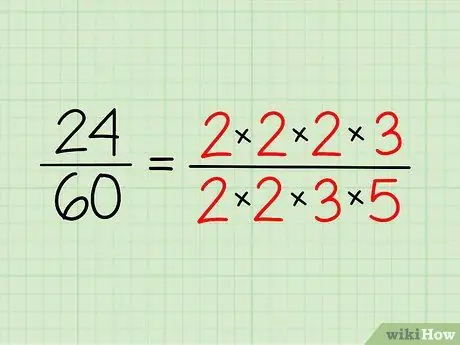
Passaggio 2. Annota la scomposizione in fattori primi di ciascun numero
Annota i numeri primi che hai per ogni numero e scrivili in forma di moltiplicazione. Non devi moltiplicarlo: è solo un modo per renderlo più facile da vedere.
- Quindi, per 24, hai 2 x 2 x 2 x 3 = 24.
- Per 60, hai 2 x 2 x 3 x 5 = 60

Passaggio 3. Elimina gli stessi fattori
Qualsiasi numero che fa parte di entrambi i numeri può essere scartato. In questo esempio, i fattori uguali sono una coppia di 2 e un 3. Arrivederci!
- Il resto sono 2 e 5 - o 2/5! La stessa risposta che abbiamo ottenuto sopra.
- Se il numeratore e il denominatore della frazione sono numeri pari, non dividere semplicemente per due. Continua a fare la divisione finché il numero che ottieni non può essere diviso di nuovo.






