Con il coefficiente di correlazione per ranghi di Spearman possiamo identificare se due variabili hanno una relazione di funzione monotona (cioè, quando un numero aumenta, anche l'altro numero aumenterà, o viceversa). Per calcolare il coefficiente di correlazione di rango di Spearman, è necessario classificare e confrontare i set di dati per trovare d2, quindi immettere i dati nella formula del coefficiente di correlazione di rango di Spearman standard o semplificata. Puoi anche calcolare questi coefficienti usando le formule di Excel o il comando R.
Fare un passo
Metodo 1 di 3: modo manuale
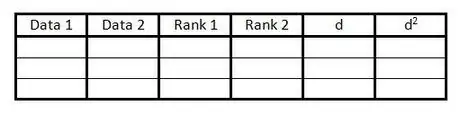
Passaggio 1. Creare una tabella
La tabella viene utilizzata per includere tutte le informazioni necessarie per calcolare il coefficiente di correlazione del rango di Spearman. Hai bisogno di una tabella come questa:
- Crea 6 colonne con intestazioni, come nell'esempio.
- Prepara tante righe vuote quante sono le coppie di dati.
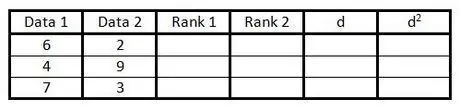
Passaggio 2. Compila le prime due colonne con le coppie di dati
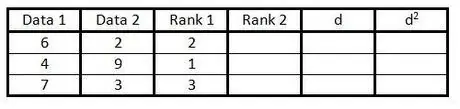
Passaggio 3. Immettere la classificazione della prima colonna dei gruppi di dati nella terza colonna da 1 a n (numero di dati)
Assegna una valutazione di 1 per il valore più basso, una valutazione di 2 per il successivo valore più basso e così via.
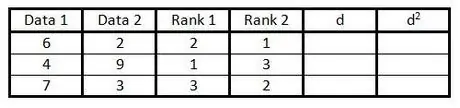
Passaggio 4. Nella quarta colonna, fai lo stesso del passaggio 3, ma per classificare i dati nella seconda colonna
-
Media_742 Se ci sono due (o più) dati che hanno lo stesso valore, calcola la valutazione media dei dati, quindi inseriscila in una tabella basata su questo valore medio.
Nell'esempio a destra, ci sono due valori di 5 sui voti 2 e 3. Poiché ci sono due 5, trova la media dei voti. La media di 2 e 3 è 2,5, quindi inserisci un valore di valutazione di 2,5 per entrambi i valori 5.
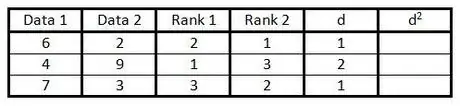
Passaggio 5. Nella colonna "d" calcolare la differenza tra i due numeri nella colonna del rango
Cioè, se una colonna è classificata 1 e l'altra colonna è classificata 3, la differenza è 2. (Il segno non ha importanza, perché il passaggio successivo è elevare il valore al quadrato).
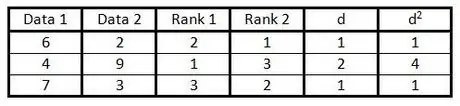
Passaggio 6. Piazza ogni numero nella colonna "d" e scrivi il risultato nella colonna "d2".
Passaggio 7. Aggiungi tutti i dati nella colonna d2".
Il risultato è d2.
Passaggio 8. Scegli una delle seguenti formule:
-
Se nessuna delle valutazioni è uguale a quella del passaggio precedente, inserisci questo valore nella formula semplificata del coefficiente di correlazione del rango di Spearman
Step8_271 e sostituire "n" con il numero di coppie di dati per ottenere il risultato.
Step9_402 -
Se è presente un rango simile nel passaggio precedente, utilizzare la formula standard del coefficiente di correlazione del rango di Spearman:
Spearman
Passaggio 9. Interpretare i risultati
Il valore può variare tra -1 e 1.
- Se il valore è vicino a -1, la correlazione è negativa.
- Se il valore è vicino a 0, non c'è correlazione lineare.
- Se il valore è vicino a 1, la correlazione è positiva.
Metodo 2 di 3: utilizzo di Excel
Passaggio 1. Creare una nuova colonna per i dati insieme alla relativa classifica
Ad esempio, se i tuoi dati si trovano nella colonna A2:A11, usa la formula "=RANK(A2, A$2:A$11)" e copiala fino a coprire tutte le colonne e le righe.
Passaggio 2. Modificare la stessa valutazione descritta nei passaggi 3 e 4 del metodo 1
Passaggio 3. Nella nuova cella, calcola la correlazione tra le due colonne di rango con la formula "= CORRELAZIONE (C2: C11, D2: D11)"
In questo esempio, C e D si riferiscono alla colonna in cui si trova la classifica. La nuova cella verrà riempita con la correlazione del rango di Spearman.
Metodo 3 di 3: utilizzo di R
Passaggio 1. Installa prima il programma R se non lo hai già
(Vedi
Passaggio 2. Salva i tuoi dati in formato CSV, inserisci i dati che desideri trovare la correlazione nelle prime due colonne
Possiamo farlo utilizzando il menu "Salva con nome".
Passaggio 3. Apri R Editor
Se stai lavorando dal terminale, esegui semplicemente R. Se stai lavorando dal desktop, fai clic sull'icona R.
Passaggio 4. Digitare il seguente comando:
- d <- read.csv("NAME_OF_YOUR_CSV.csv") e premi Invio.
- cast(rank(d[, 1]), rank(d[, 2]))
Suggerimenti
I dati devono essere composti da almeno 5 coppie in modo che il trend possa essere visto (il numero di dati è 3 coppie nell'esempio solo per semplificare i calcoli)
Avvertimento
- Il coefficiente di correlazione del rango di Spearman identifica solo la forza della correlazione in cui i dati aumentano o diminuiscono in modo coerente. Se c'è un'altra tendenza nei dati, la correlazione di rango di Spearman no fornirà una rappresentazione accurata.
- Questa formula si basa sul presupposto che non vi siano valutazioni uguali. Quando c'è lo stesso rango dell'esempio, dovremmo usare questa definizione: il coefficiente di correlazione del momento di moltiplicazione per rango.
