- Autore Jason Gerald [email protected].
- Public 2024-01-15 08:17.
- Ultima modifica 2025-06-01 06:06.
Potresti pensare che gli interi siano solo numeri ordinari, come 3, -12, 17, 0, 7000 o -582. Gli interi sono anche chiamati numeri interi perché non sono divisi in parti come frazioni e decimali. Leggi questo articolo per imparare tutto ciò che ti serve sull'aggiunta e la sottrazione di numeri interi, oppure leggi direttamente la sezione che ti serve.
Fare un passo
Metodo 1 di 5: aggiunta e sottrazione di numeri interi positivi utilizzando una linea numerica

Passaggio 1. Comprendere la linea dei numeri
Le linee dei numeri trasformano la matematica di base in qualcosa di tangibile e fisico che puoi vedere. Con pochi segni e buon senso, possiamo usarlo come una calcolatrice per aggiungere e sottrarre numeri.

Passaggio 2. Disegna una linea numerica di base
Immagina o disegna una linea retta uniforme. Fai un punto nel mezzo della tua linea. Scrivi 0 o zero accanto a questo periodo.
Il tuo libro di matematica potrebbe chiamarlo il punto di partenza perché è il punto di partenza per tutti i numeri

Passaggio 3. Disegna due punti, uno a destra e uno a sinistra del tuo zero
Scrivi - 1 accanto al punto a sinistra e
Passo 1. accanto al punto a destra. Questo è l'intero più vicino a zero.
- Non preoccuparti di rendere le distanze tra i punti esattamente uguali: se sai cosa significa ogni punto, puoi usare una linea dei numeri.
- Il lato sinistro è l'inizio della frase.

Passaggio 4. Completa la riga dei numeri aggiungendo più numeri
Crea più punti a sinistra di -1 e a destra di 1. A sinistra, da -1, segna i tuoi punti con - 2, - 3, e - 4. A destra, da 1, segna il tuo punto con
Passo 2
Passaggio 3., da
Passaggio 4.. Puoi continuare se hai spazio sul foglio.
L'esempio nella figura mostra una linea numerica da -6 a 6

Passaggio 5. Comprendere gli interi positivi e negativi
Interi positivi, chiamati anche numero naturale, è un numero intero maggiore di zero. 1, 2, 3, 25, 99 e 2007 sono numeri interi positivi. Gli interi negativi sono numeri interi minori di zero (come -2, -4 e -88).
I numeri interi sono un altro modo per chiamare numeri interi. Frazioni come 1/2 (metà) sono solo una parte del numero, quindi non sono numeri interi. Uguale al decimale, ad esempio 0,25 (zero virgola due cinque); decimale non è un numero intero

Passaggio 6. Inizia a risolvere 1+2 posizionando il dito sul punto 1
Risolveremo semplici problemi di addizione 1+2 utilizzando la linea dei numeri appena creata. Il primo numero è
Passo 1., quindi inizia a mettere il dito sul numero.
-
Questa domanda è troppo facile?
Se hai mai aggiunto, probabilmente conosci la risposta a 1+2. Bene: se conosci il risultato, sarà più facile capire come funziona la linea dei numeri. Quindi, puoi usare la linea dei numeri per risolvere problemi di addizione più difficili o prepararti per la matematica più difficile come l'algebra.

Passaggio 7. Somma 1+2 spostando il dito di 2 punti a destra
Fai scorrere il dito verso destra, contando il numero di punti (un altro numero) che passi. Se hai superato 2 nuovi punti, fermati. Il numero puntato dal tuo dito è la risposta,
Passaggio 3
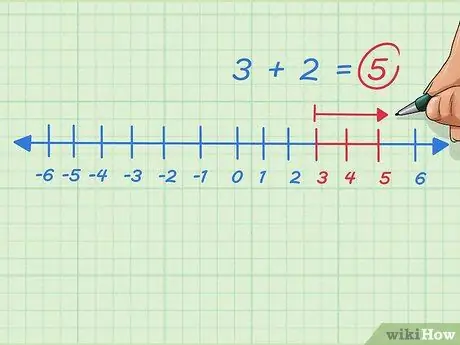
Passaggio 8. Aggiungi eventuali numeri interi positivi spostandoti a destra sulla linea dei numeri
Supponiamo di voler risolvere 3+2. Inizia da 3, spostati a destra o aggiungi 2 punti. Ci fermiamo a 5. Il problema si scrive 3 + 2 = 5.

Passaggio 9. Sottrarre numeri interi positivi spostandosi a sinistra sulla linea dei numeri
Ad esempio, vogliamo risolvere 6 -4, iniziamo da 6, ci spostiamo a sinistra di 4 punti e ci fermiamo a 2. Questo problema si scrive 6 - 4 = 2.
Metodo 2 di 5: aggiunta e sottrazione di numeri negativi utilizzando una linea numerica

Passaggio 1. Ulteriori informazioni sulle linee dei numeri
Se non sai come creare una linea numerica, torna alla sezione Addizione e sottrazione di numeri positivi utilizzando le linee numeriche per imparare a crearne una.
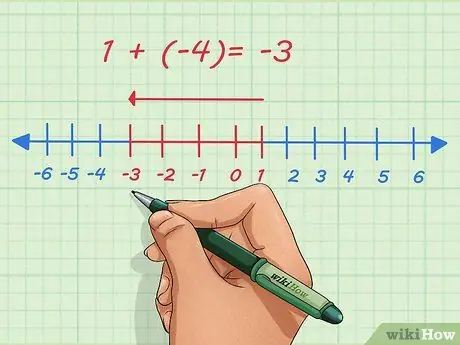
Passaggio 2. Comprendere i numeri negativi
I numeri positivi sono indicati dalla direzione a destra sulla linea dei numeri. I numeri negativi sono indicati a sinistra sulla linea dei numeri. Aggiungere numeri negativi significa spostare il punto a sinistra sulla linea dei numeri.
-
Ad esempio, aggiungiamo 1 e -4. Di solito, questa domanda è scritta così:
1 + (-4)
. Sulla linea dei numeri, iniziamo da 1, ci spostiamo di 4 punti a sinistra e ci fermiamo a -3.
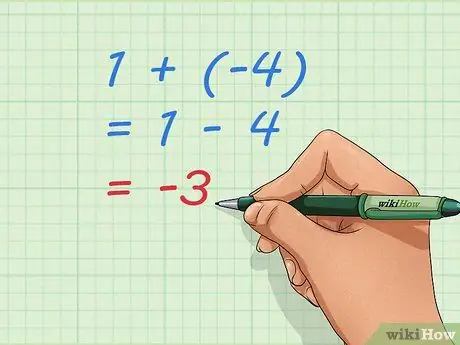
Passaggio 3. Utilizzare le equazioni di base per comprendere l'aggiunta di numeri negativi
Nota che -3, la nostra risposta, è il numero che otterremo se facciamo 1 - 4. Sommare 1 + (-4) e sottrarre 4 da 1 è lo stesso problema. Possiamo scriverlo come un'equazione, una frase matematica che mostra l'uguaglianza:1 + (-4) = 1 - 4 = -3
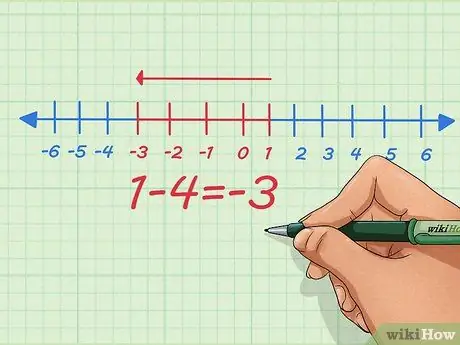
Passaggio 4. Invece di aggiungere numeri negativi, trasformalo in un problema di sottrazione utilizzando numeri positivi
Come possiamo vedere dalla semplice equazione sopra, possiamo fare entrambe le cose: trasformare l'aggiunta di numeri negativi in sottrazione di numeri positivi e viceversa. Potrebbe esserti stato insegnato a trasformare i negativi in negativi senza sapere perché - ecco perché.
-
Ad esempio, -4. Quando aggiungiamo -4 e 1, sottraiamo 1 per 4. Può essere scritto in matematica scrivendo
1 + (-4) = 1 - 4
. Possiamo scriverlo sulla linea dei numeri, partendo dal nostro punto di partenza da 1, quindi aggiungendo 4 punti a sinistra (in altre parole, aggiungendo -4). Poiché questa è un'equazione, una cosa è uguale a un'altra, quindi è vero anche il contrario
1 - 4 = 1 + (-4)
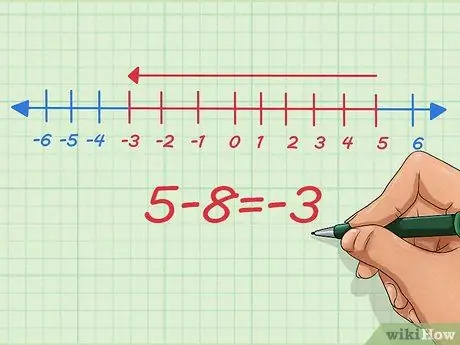
Passaggio 5. Capire come sottrarre numeri negativi su una linea dei numeri
Sulla linea dei numeri, sottrarre numeri negativi equivale a ridurre la lunghezza. Iniziamo con 5 - 8.
Sulla linea dei numeri, iniziamo dal nostro punto di partenza da 5, sottraiamo 8 e ci fermiamo a -3
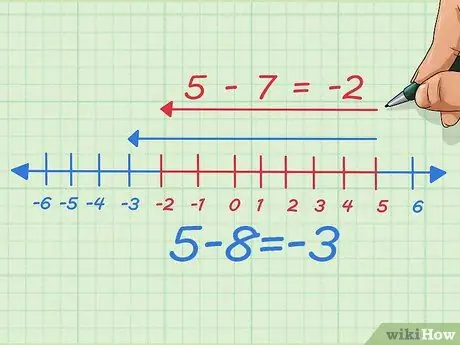
Passaggio 6. Sottrai l'importo che stai sottraendo e guarda cosa succede
Supponiamo di sottrarre uno, il numero che sottraiamo, o in altre parole sottrarre 7 invece di 8. Ora sottraiamo un punto a sinistra sulla linea dei numeri. Per iscritto, abbiamo iniziato con 5 - 8 = -3 Ora spostiamo solo 7 a sinistra, quindi diventa 5 - 7 = -2
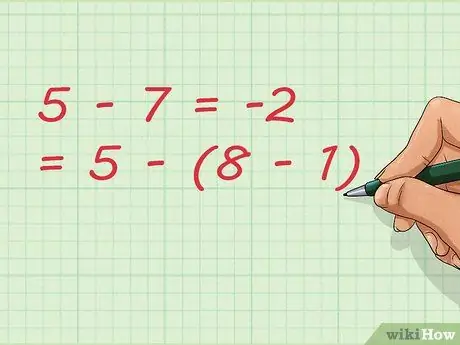
Passaggio 7. Notare che la sottrazione può comportare un'aggiunta
Nel nostro esempio, stiamo sottraendo il numero 1. Nello scrivere l'equazione, possiamo scriverla più corta come: 5 - 7 = -2 = 5 - (8 - 1)

Passaggio 8. Converti i segni negativi in positivi quando aggiungi numeri negativi
Utilizzando il passaggio di convertire tutte le sottrazioni in addizioni, possiamo scriverne di più brevi come: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Sappiamo già che 5 - 8 = -3, quindi prendi 5 - 8 dall'equazione e inserisci -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Sappiamo già che 5 - (8 - 1) è - sottrae un punto da 5 - 8. La nostra equazione può mostrare che 5 - 8 è uguale a -3, e sottraendo un punto dà -2. L'equazione può essere scritta così:
-3 - (-1) = -3 + 1
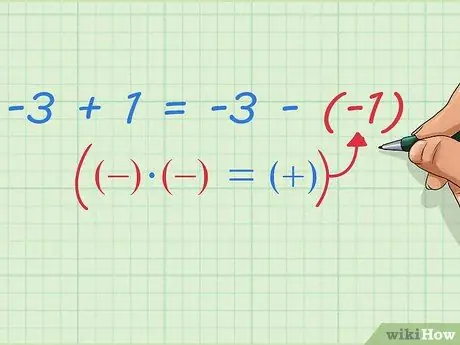
Passaggio 9. Scrivi la sottrazione dei numeri negativi come addizione
Nota cosa succede dopo questo - abbiamo già dimostrato che: -3 + 1 = -3 - (-1) Possiamo scrivere questo con regole di scrittura matematica più semplici e generali: primo numero più il secondo numero = primo numero meno (secondo numero negativo) Oppure, un modo più semplice che probabilmente hai sentito durante le lezioni di matematica: Cambia i due segni negativi in un segno positivo.
Metodo 3 di 5: aggiunta di numeri interi grandi positivi

Passaggio 1. Scrivi il problema di addizione di 2.503 + 7.461 con un numero sopra l'altro
Annota i numeri nella colonna grande in modo che 2 sia maggiore di 7, 5 maggiore di 4 e così via. In questo modo impareremo come aggiungere numeri interi troppo grandi per immaginare o utilizzare la linea dei numeri.
Scrivi un segno + a sinistra del numero sottostante e della riga sotto di esso, come potresti imparare per problemi di addizione più piccoli
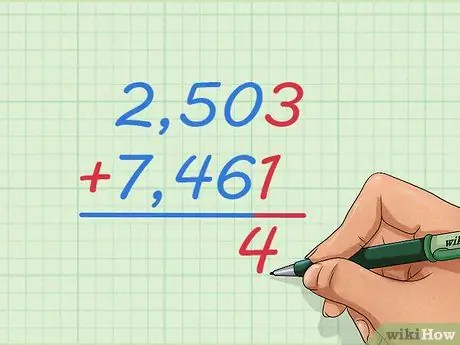
Passaggio 2. Inizia sommando i due numeri all'estrema destra
Potrebbe essere un po' strano iniziare da destra perché leggiamo i numeri da sinistra. Dobbiamo aggiungere da destra per ottenere la risposta corretta, che puoi vedere in seguito.
-
Sotto i due numeri più a destra,
Passaggio 3. da
Passo 1., scrivi la somma dei due
Passaggio 4..

Passaggio 3. Somma ogni numero nella colonna allo stesso modo
Sposta a sinistra, somma 0+6, 5+4, e 2+7. Scrivi la risposta sotto ogni coppia di numeri.
La tua risposta dovrebbe essere: 9.964. Controlla il tuo lavoro se commetti un errore.

Passaggio 4. Ora somma 857+135
Noterai qualcosa di diverso non appena sommi la prima coppia di numeri a destra. 7+5 è uguale a 12, un numero di due cifre, ma puoi scrivere solo una cifra sotto quella colonna. Continua a leggere per scoprire cosa dovresti fare e perché dovresti sempre partire da destra e non da sinistra.

Passaggio 5. Somma 7+5 e scopri dove scrivere la risposta
7+5=12, ma non puoi mettere 1 e 2 sotto la linea. Ma, scrivi l'ultima cifra, Passo 2., sotto la riga e scrivi la prima cifra
Passo 1., sopra la colonna a sinistra, 5+3.
-
Se sei curioso di sapere come funziona, pensa a cosa significa dividere 1 e 2. In realtà stai dividendo 12 in
Passaggio 10. da
Passo 2.. Se vuoi, puoi scrivere 10 sopra il numero e vedrai 1 nelle colonne 5 e 3, proprio come prima.

Passaggio 6. Somma 1+5+3 per ottenere la cifra successiva della risposta
Ora hai tre cifre da sommare perché hai aggiunto 1 a questa colonna. La risposta è
Passaggio 9., quindi la tua risposta diventa 92.
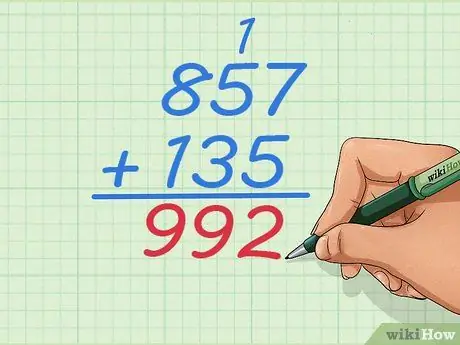
Passaggio 7. Completa il problema come al solito
Continua a lavorare le cifre a sinistra finché non hai sommato tutti i numeri, in questo caso, rimane solo una colonna. La tua risposta finale dovrebbe essere 992.
- Puoi provare domande più complicate, come 974+568. Ricorda, ogni volta che ottieni un numero a due cifre, scrivi solo l'ultima cifra come risposta e posiziona l'altra cifra sopra la colonna a sinistra, che aggiungerai dopo. Se la risposta nell'ultima colonna (all'estrema sinistra) contiene due cifre, scrivila come risposta.
- Vedi la sezione Suggerimenti per le risposte alle domande 974+568 una volta che hai provato a risolverle.
Metodo 4 di 5: sottrazione di numeri interi positivi grandi

Passaggio 1. Scrivi il problema di sottrazione 4.713 - 502 con il primo numero sopra il secondo numero
Scrivilo in modo che 3 sia direttamente sopra 2, 1 sia sopra 0, 7 sia sopra 5 e 4 sia sopra lo spazio vuoto.
Puoi scrivere 0 sotto 4 se questo ti aiuta a ricordare quale numero è sopra quale numero. Puoi sempre aggiungere uno 0 davanti a un numero senza modificarlo. Assicurati di aggiungerlo prima del numero, non dopo

Passaggio 2. Sottrai ogni numero sottostante dal numero direttamente sopra di esso
Inizia sempre da destra. Risolvi 3-2, 1-0, 7-5 e 4-0, scrivi la risposta a ciascuna domanda direttamente sotto i due numeri sottratti.
Il risultato è, 4.211.

Passaggio 3. Ora scrivi le domande 924 - 518 allo stesso modo
Questi numeri hanno lo stesso numero di cifre, quindi puoi scriverli facilmente. Questo problema ti insegnerà qualcosa sulla sottrazione di numeri interi se non lo sai già.

Passaggio 4. Scopri come risolvere il primo problema, che si trova all'estrema destra
4 - 8. Questo problema è complicato perché 4 è minore di 8, ma non utilizzare numeri negativi, ma segui questi passaggi:
- Nella riga in alto, incrocia 2 e scrivi 1. 2 dovrebbe essere a sinistra di 4.
- Incrocia 4 e scrivi 14. Fallo in uno spazio stretto in modo che sia chiaro che 14 è più di 8. Puoi anche scrivere 1 davanti a 4 per fare 14 se c'è abbastanza spazio.
- Quello che hai appena fatto è prendere in prestito 1 dal posto delle decine o dalla seconda colonna da destra e convertirlo in 10 al posto delle unità o nella colonna all'estrema destra. Una volta che il numero 10 è uguale a dieci volte il numero 1, quindi è lo stesso.

Passaggio 5. Ora risolvi i problemi 14 - 8 e scrivi la risposta nella colonna più a destra
Avrebbe dovuto scrivere 6 sulla riga di risposta più a destra.

Passaggio 6. Completa la colonna successiva a sinistra, utilizzando il nuovo numero che hai annotato
La sottrazione dovrebbe essere 1 - 1, che è uguale a 0.
La tua risposta ora dovrebbe essere 06.

Passaggio 7. Risolvi il problema completando l'ultima sottrazione, la colonna più a sinistra
9 - 5 = 4, quindi la tua risposta finale è 406.

Passaggio 8. Ora risolviamo il problema di sottrarre numeri grandi da numeri piccoli
Supponiamo che ti venga chiesto di completare 415.990 - 968.772. Scrivi il secondo numero sotto il primo numero e ti renderai conto che il numero sotto è più grande! Puoi dire immediatamente dalla prima cifra a sinistra: 9 è maggiore di 4, quindi i numeri che iniziano con 9 sono più grandi.
Assicurati di scrivere correttamente la colonna prima di confrontare. 912 no maggiore di 5000 puoi dire se scrivi correttamente la colonna perché non ci sono numeri sotto 5. Puoi aggiungere zero help, ad esempio, scrivi 912 con 0912 in modo che la colonna sia uguale a 5000.

Passaggio 9. Scrivi il numero più piccolo sotto il numero più grande e aggiungi un segno - davanti alla risposta
Ogni volta che si sottrae un numero da un numero più piccolo, il risultato è un numero negativo. È meglio scrivere questo segno prima di sottrarre in modo da non dimenticare di scriverlo.

Passaggio 10. Per rispondere, sottrarre il numero piccolo dal numero grande e ricordarsi di scrivere il segno -
La tua risposta sarà negativa, che è indicata da un segno -. Non cerca di sottrarre un numero grande da un numero piccolo, quindi rende il risultato negativo; la tua risposta sarà sbagliata.
Il nuovo problema da risolvere è: 968.772 - 415.990 = -? Vedere la sezione Suggerimenti per la risposta dopo aver provato a risolvere questo problema
Metodo 5 di 5: aggiunta e sottrazione di numeri interi negativi
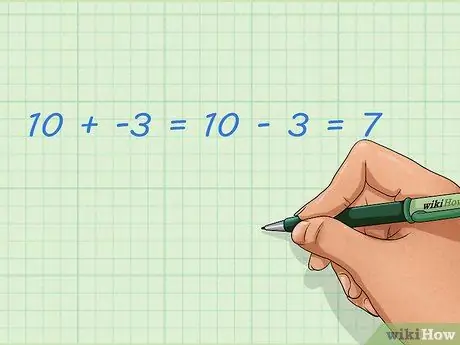
Passaggio 1. Impara come aggiungere numeri negativi e positivi
Aggiungere numeri interi negativi equivale a sottrarre numeri interi positivi. Questo è più facile da fare con la linea dei numeri descritta in un'altra sezione, ma puoi pensarci anche a parole. I numeri negativi non sono numeri ordinari; questo numero è minore di zero e può rappresentare l'importo prelevato. Se aggiungi questa ripresa a un numero normale, il risultato diventa più piccolo.
- Esempio: 10 + -3 = 10 - 3 = 7
- Esempio: -12 + 18 = 18 + -12 = 18 - 12 = 6. Ricorda che puoi sempre modificare l'ordine dei numeri in aggiunta, ma non in sottrazione.
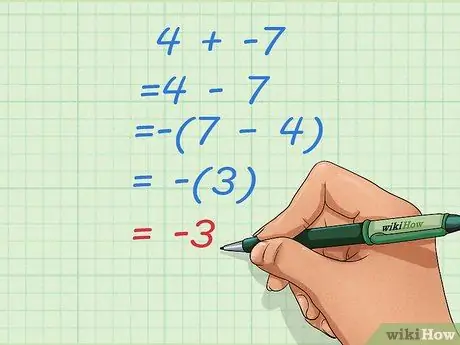
Passaggio 2. Impara cosa devi fare se lo trasformi in un problema di sottrazione con un numero iniziale più piccolo
A volte, cambiare l'addizione ai problemi di sottrazione come quello sopra può portare a risposte dispari come 4 - 7. Quando ciò accade, invertire l'ordine dei numeri e rendere il risultato negativo.
- Diciamo che il tuo problema iniziale è 4 + -7.
- Trasformalo in un problema di sottrazione: 4 - 7
- Invertire l'ordine e rendere negativo il risultato: -(7 - 4) = -(3) = -3.
- Se non hai familiarità con l'uso delle parentesi nelle equazioni, pensa a questo: 4 - 7 si trasforma in 7 - 4 con l'aggiunta di un segno negativo. 7 - 4 = 3, ma dobbiamo cambiarlo in -3 in modo che la risposta alle domande 4 - 7 sia corretta.
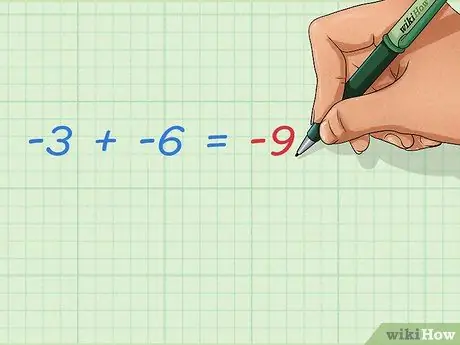
Passaggio 3. Impara come aggiungere due numeri interi negativi
Due numeri negativi aggiunti aumentano sempre il risultato negativo. Poiché non vengono aggiunti numeri positivi, il risultato sarà più lontano da 0. La risposta è semplice:
- -3 + -6 = -9
- -15 + -5 = -20
- Vedi lo schema? Tutto quello che devi fare è sommare i numeri come se fossero numeri positivi e aggiungere un segno negativo. -4 + -3 = -(4 + 3) = -7
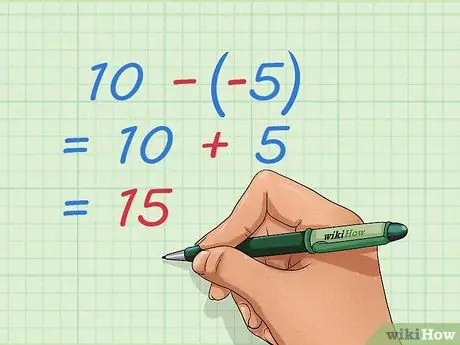
Passaggio 4. Impara a sottrarre numeri interi negativi
Come il problema dell'addizione, puoi riscrivere il problema in modo da avere solo numeri positivi. Se sottrai i numeri negativi, togli alcune delle cose che sono già state prese, il che equivale ad aggiungere numeri positivi.
- Pensa ai numeri negativi come denaro rubato. Se sottrai o togli denaro rubato per poterlo restituire, è come dare soldi a qualcuno, giusto?
- Esempio: 10 - -5 = 10 + 5 = 15
- Esempio: -1 - -2 = -1 + 2. Hai già imparato a risolvere questo problema nel primo passaggio, ricordi? Rileggi come aggiungere numeri negativi e positivi se hai dimenticato.
- Ecco la soluzione completa dell'ultimo esempio: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Suggerimenti
- Potresti aver scritto numeri lunghi come 2.521.301 usando le virgole (,) invece di (.) a seconda di dove vivi. Usa ciò che ti chiede il tuo insegnante in modo da non confonderti con altri sistemi di scrittura.
- Disegna le tue linee numeriche su scale diverse per rappresentare numeri diversi. Non c'è una regola per cui ogni distanza su una linea dei numeri sia uguale a 1. Immagina una linea dei numeri che è 10 invece di 1. A parte il fatto che ogni punto è 10 ora, l'addizione e la sottrazione rimangono le stesse. Provalo se non ci credi.
- Se provi le domande speciali della sfida nella sezione Numeri lunghi, ecco la risposta: 974 + 568 = 1.542. La risposta da 415.990 a 968.772 è - 552.782.






