- Autore Jason Gerald [email protected].
- Public 2023-12-16 11:19.
- Ultima modifica 2025-01-23 12:21.
L'aggiunta di frazioni è una conoscenza molto utile. Questa abilità è molto facile da imparare e utilizzare quando si lavora su problemi di matematica dalle elementari alle superiori. Questo articolo spiega come aggiungere le frazioni in modo da poterlo fare in pochi minuti.
Fare un passo
Metodo 1 di 2: aggiunta di frazioni con lo stesso denominatore

Passaggio 1. Controlla il denominatore (il numero sotto il quoziente) di ogni frazione
Se i numeri sono gli stessi, stai aggiungendo frazioni con lo stesso denominatore. Se i denominatori sono diversi, leggi il secondo metodo.
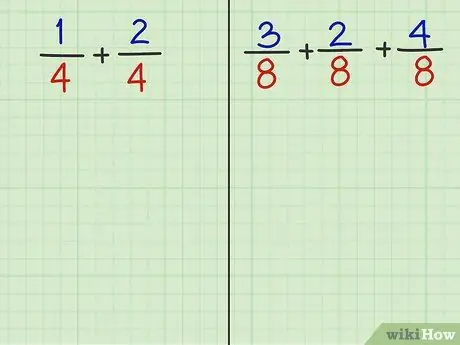
Passaggio 2. Rispondi alle seguenti 2 domande
Leggendo l'ultimo passaggio di questo metodo, dovresti essere in grado di sommare le frazioni delle seguenti due domande.
- Problema 1: 1/4 + 2/4
- Problema 2: 3/8 + 2/8 + 4/8
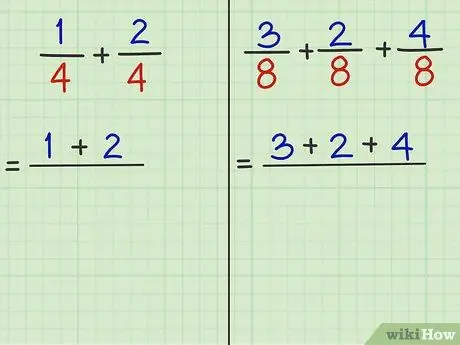
Passaggio 3. Raccogli i numeratori (i numeri sopra la divisione) e sommali
Il numeratore è il numero sopra il quoziente. Non importa quante frazioni vuoi aggiungere, puoi aggiungere subito i numeratori se i denominatori sono gli stessi.
- Problema 1: 1/4 + 2/4 è la frazione da aggiungere. "1" e "2" sono numeratori. Quindi, 1 + 2 = 3.
- Problema 2: 3/8 + 2/8 + 4/8 è la frazione da sommare. "3" e "2" e "4" sono numeratori. Quindi, 3 + 2 + 4 = 9.

Passaggio 4. Determinare la nuova frazione dalla somma
Annotare il numeratore ottenuto nel passaggio 2. Questo numero è nuovo numeratore. Scrivi il denominatore, che è lo stesso numero sotto la bisettrice di ogni frazione. Non è necessario eseguire i calcoli se i denominatori sono gli stessi. Questo numero è nuovo denominatore ed è sempre uguale al vecchio denominatore quando aggiungi frazioni con lo stesso denominatore.
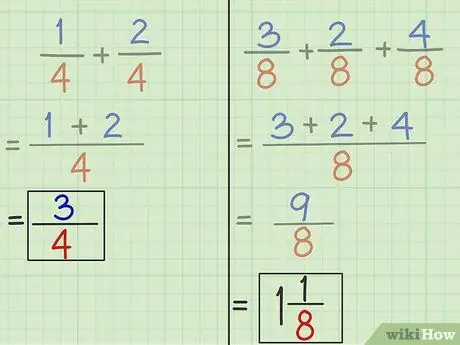
- Problema 1: 3 è il nuovo numeratore e 4 è il nuovo denominatore. Pertanto, la risposta alla domanda 1 è 3/4. 1/4 + 2/4 = 3/4.
- Problema 2: 9 è il nuovo numeratore e 8 è il nuovo denominatore. Pertanto, la risposta alla domanda 2 è 9/8. 3/8 + 2/8 + 4/8 = 9/8.
Passaggio 5. Semplificare le frazioni se necessario
Non dimenticare di semplificare la nuova frazione per rendere più semplice la scrittura.
-
Se il numeratore più grande invece di un denominatore come il risultato dell'addizione del problema 2, questo significa che otteniamo 1 mese intero dopo aver semplificato la frazione. Dividi il numeratore per il denominatore o 9 diviso per 8. Il risultato è un intero 1 rimanente 1. Scrivi interi davanti alla frazione e il resto diventa il numeratore di una nuova frazione con lo stesso denominatore.
9/8 = 1 1/8.
Metodo 2 di 2: aggiunta di frazioni con diversi denominatori

Passaggio 1. Controlla il denominatore (il numero sotto il quoziente) di ogni frazione
Se i denominatori sono diversi, sei sommare frazioni con denominatori diversi. Leggi i seguenti passaggi perché devi rendere uguali i denominatori prima di aggiungere le frazioni.
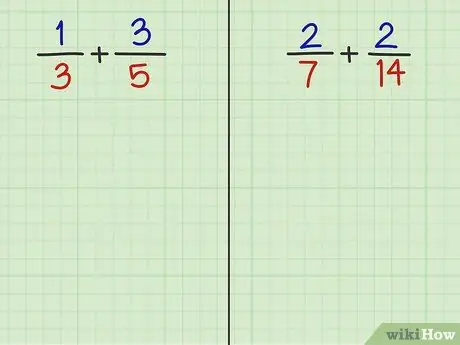
Passaggio 2. Risolvi le seguenti 2 domande
Leggendo l'ultimo passaggio di questo metodo, dovresti essere in grado di sommare le frazioni delle seguenti due domande.
- Problema 3: 1/3 + 3/5
- Domanda 4: 2/7 + 2/14

Passaggio 3. Abbina i denominatori
Per fare ciò, moltiplica i denominatori delle due frazioni sopra. Un modo semplice per equalizzare i denominatori è moltiplicare i denominatori delle due frazioni. Se uno dei denominatori è multiplo dell'altro, trova il minimo comune multiplo dei due denominatori.
-
Problema 3:
3 x 5 = 15. Quindi, il nuovo denominatore di entrambe le frazioni è 15.
-
Problema 4:
14 è un multiplo di 7. Pertanto, dobbiamo solo moltiplicare 7 per 2 per ottenere 14. Pertanto, il nuovo denominatore di entrambe le frazioni è 14.

Passaggio 4. Moltiplica il numeratore e il denominatore della prima frazione per il denominatore della seconda frazione
Questo passaggio non cambia il valore della frazione, ma la frazione sembra cambiare per corrispondere al denominatore. Il valore frazionario rimane lo stesso.
-
Problema 3:
1/3 x 5/5 = 5/15.
-
Problema 4:
Per questo problema, dobbiamo solo moltiplicare la prima frazione per 2/2 per ottenere i denominatori uguali.
2/7 x 2/2 = 4/14

Passaggio 5. Moltiplica il numeratore e il denominatore della seconda frazione per il denominatore della prima frazione
Simile ai passaggi precedenti, non cambiamo il valore della frazione, ma la frazione sembra cambiare per equalizzare il denominatore. Il valore frazionario rimane lo stesso.
-
Problema 3:
3/5 x 3/3 = 9/15.
-
Problema 4:
Non abbiamo bisogno di moltiplicare la seconda frazione perché i denominatori sono gli stessi.

Passaggio 6. Scrivi le due nuove frazioni in ordine
A questo punto, non abbiamo sommato le due frazioni, anche se possiamo. Nel passaggio precedente, abbiamo moltiplicato ogni frazione per 1. Ora, vogliamo assicurarci che le frazioni che vogliamo aggiungere abbiano lo stesso denominatore.
-
Problema 3:
invece di 1/3 + 3/5, la frazione diventa 5/15 + 9/15
-
Problema 4:
Invece di 2/7 + 2/14, la frazione diventa 4/14 + 2/14

Passaggio 7. Somma i numeratori delle due frazioni
Il numeratore è il numero sopra il quoziente.
-
Problema 3:
5 + 9 = 14. 14 è il nuovo numeratore.
-
Problema 4:
4 + 2 = 6. 6 è il nuovo numeratore.

Passaggio 8. Scrivi il denominatore comune (nel passaggio 2) sotto il nuovo numeratore o usa il denominatore della frazione moltiplicato per 1 per equalizzare il denominatore
-
Problema 3:
15 è il nuovo denominatore.
-
Problema 4:
14 è il nuovo denominatore.

Passaggio 9. Scrivi un nuovo numeratore e un nuovo denominatore
-
Problema 3:
14/15 è la risposta 1/3 + 3/5 = ?
-
Problema 4:
6/14 è la risposta 2/7 + 2/14 = ?

Passaggio 10. Semplifica e riduci le frazioni
Per semplificare le frazioni, dividi numeratore e denominatore per il massimo comun divisore dei due numeri.
-
Problema 3:
14/15 non può essere semplificato.
-
Problema 4:
6/14 può essere ridotto a 3/7 dividendo numeratore e denominatore per 2 come massimo comun divisore di 6 e 14.
Suggerimenti
- Prima di sommare le frazioni, assicurati che i denominatori siano gli stessi.
- Non sommare i denominatori. Se i denominatori sono gli stessi, usa il numero come denominatore dopo aver sommato le frazioni.
- Se vuoi aggiungere frazioni con numeri che consistono di numeri interi e frazioni, converti quei numeri in frazioni e sommali secondo le istruzioni sopra.






