Nelle statistiche, l'intervallo è la differenza tra il valore più alto in un set di dati e il valore più basso in un set di dati. L'intervallo mostra quanto sono distribuiti i valori in una serie. Se l'intervallo è un numero elevato, i valori nella serie sono altamente dispersi; se l'intervallo è un numero piccolo, i valori nella serie sono vicini l'uno all'altro. Se vuoi sapere come calcolare la copertura, segui questi passaggi.
Fare un passo
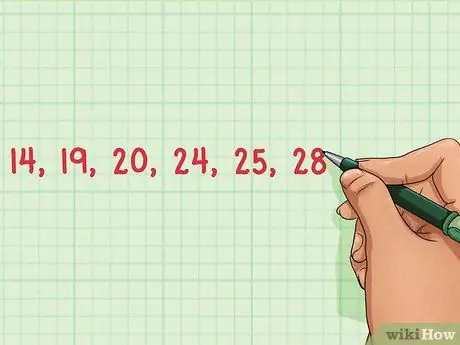
Passaggio 1. Elenca gli elementi del tuo set di dati
Per trovare l'intervallo di un set di dati, è necessario elencare tutti gli elementi nel set di dati in modo da poter identificare i numeri più grandi e più piccoli. Annota tutti gli elementi. I numeri in questo set di dati sono: 14, 19, 20, 24, 25 e 28.
- È più facile identificare i numeri più grandi e più piccoli in un set di dati se si ordinano i numeri dal più piccolo al più grande. In questo esempio, il set di dati sarebbe strutturato in questo modo: 14, 19, 20, 24, 24, 25, 28.
- L'ordinamento degli elementi in un set di dati ti aiuterà anche a eseguire altri calcoli, come trovare la modalità, la media o la mediana del set di dati.
Passaggio 2. Identificare i numeri più grandi e più piccoli nel set di dati
In questo problema, il numero più piccolo nel set di dati è 14 e il numero più grande è 28.
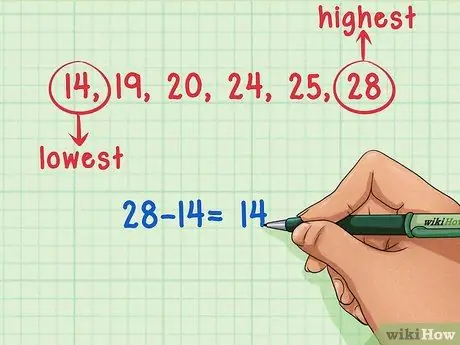
Passaggio 3. Sottrai il numero più piccolo nel tuo set di dati dal numero più grande
Ora che hai identificato i numeri più piccoli e più grandi nel set di dati, tutto ciò che devi fare è sottrarli l'uno dall'altro. Sottrai 14 da 25 (25 – 14) per ottenere 11, l'intervallo del set di dati.
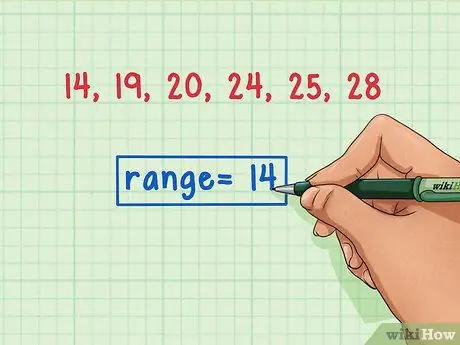
Passaggio 4. Etichettare chiaramente l'intervallo
Una volta trovato l'intervallo, etichettalo chiaramente. Questo ti aiuterà a evitare confusione con altri calcoli statistici che potresti dover eseguire, come trovare la mediana, la modalità o la media.
Suggerimenti
- Puoi anche interpretare l'intervallo in termini algebrici, ma devi prima comprendere il concetto di funzione algebrica o un insieme di operazioni su numeri noti. Poiché le operazioni sulle funzioni possono essere eseguite su qualsiasi numero, anche sconosciuto, il numero è indicato da una variabile letterale, solitamente x. Un dominio è un insieme di possibili valori di input, che puoi sostituire con il numero sconosciuto. Pertanto, l'intervallo è l'insieme dei possibili risultati di calcolo, che si ottengono dopo aver inserito uno dei valori del dominio e aver completato tutte le operazioni definite dalla funzione. Sfortunatamente, non c'è modo di calcolare l'intervallo di una funzione. A volte, rappresentare graficamente una funzione o calcolare più valori può mostrare uno schema chiaro. Puoi anche usare la tua conoscenza del dominio della funzione per scartare i possibili valori di output (risultati di calcolo) o restringere il set di dati che rappresenta l'intervallo.
- Il valore mediano di qualsiasi set di dati statistici rappresenta il valore mediano del set di dati in termini di distribuzione dei dati, non di intervallo. Quindi, mentre potresti voler assumere che la mediana di un dato set di dati sia l'intervallo diviso per 2 - o metà dell'intervallo dell'intervallo - questo di solito non è vero. Per trovare la mediana corretta, è necessario ordinare gli elementi dei dati, quindi cercare l'elemento al centro dell'elenco. Questo elemento è la mediana. Ad esempio, se hai un elenco di 29 elementi, il quindicesimo elemento ha lo stesso intervallo dall'inizio dell'elenco e dalla fine dell'elenco, quindi il quindicesimo elemento è la mediana, indipendentemente da come il valore di quell'elemento si riferisce a la gamma.
