- Autore Jason Gerald [email protected].
- Public 2024-01-16 19:37.
- Ultima modifica 2025-01-23 12:21.
Nello studio degli strumenti ottici, l'"ingrandimento" di un oggetto simile a una lente è il rapporto tra l'altezza dell'immagine che si vede e l'altezza effettiva dell'oggetto. Ad esempio, una lente che può far sembrare un oggetto molto grande ha un fattore di ingrandimento "alto", mentre una lente che fa sembrare un oggetto piccolo ha un fattore di ingrandimento "basso". La formula per l'ingrandimento di un oggetto viene solitamente calcolata utilizzando la formula M = (hio/ho) = -(dio/Do), dove M = ingrandimento, hio = altezza dell'immagine, ho = altezza dell'oggetto, e dio e Do = distanza dell'immagine e dell'oggetto.
Fare un passo
Metodo 1 di 2: Calcolo dell'ingrandimento dell'obiettivo singolo
Note: A lente convergente più largo al centro che ai bordi (come una lente d'ingrandimento). un lente divergente più largo ai bordi che al centro (come una ciotola). Il calcolo dell'ingrandimento su entrambi gli obiettivi è lo stesso, con un'eccezione importante. Clicca qui per andare direttamente alle eccezioni alle lenti divergenti.
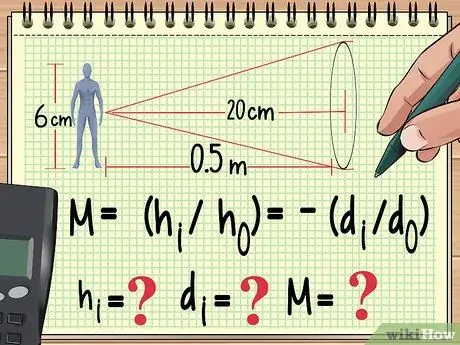
Passaggio 1. Inizia con la tua equazione e le variabili che già conosci
Proprio come qualsiasi altro problema di fisica, il modo per risolvere un problema di ingrandimento è scrivere l'equazione che utilizzerai per calcolarlo. Da qui, puoi lavorare a ritroso per trovare il valore della variabile che non hai trovato dall'equazione che stai utilizzando.
-
Ad esempio, supponiamo che una bambola alta 6 cm sia posta a un metro da a lente convergente con una lunghezza focale di 20 cm. Se vogliamo calcolare l'ingrandimento, l'altezza dell'immagine e la distanza dell'immagine, possiamo iniziare a scrivere la nostra equazione come segue:
-
- M = (hio/ho) = -(dio/Do)
-
- Ora sappiamo ho (altezza della bambola) e do (distanza della bambola dall'obiettivo). Conosciamo anche la lunghezza focale dell'obiettivo, che non è in questa equazione. conteremo hio, Dioe M.

Passaggio 2. Utilizzo dell'equazione dell'obiettivo per ottenere dio.
Se conosci la distanza dall'oggetto che stai ingrandendo e la lunghezza focale dell'obiettivo, calcolare la distanza dall'immagine formata è molto semplice con l'equazione dell'obiettivo. L'equazione della lente è 1/f = 1/do + 1/dio, dove f = lunghezza focale dell'obiettivo.
-
In questo problema di esempio, possiamo usare l'equazione della lente per calcolare dio. Inserisci i valori di f e dio quindi risolvi l'equazione:
-
- 1/f = 1/do + 1/dio
- 1/20 = 1/50 + 1/dio
- 5/100 - 2/100 = 1/dio
- 3/100 = 1/dio
- 100/3 = dio = 33,3 cm
-
- La lunghezza focale dell'obiettivo è la distanza dal centro dell'obiettivo al punto in cui la luce viene trasmessa nel punto focale. Se hai mai focalizzato la luce con una lente d'ingrandimento sulle formiche in fiamme, l'hai visto. Nelle domande della lezione, di solito è stata data l'entità di questo hotspot. Nella vita reale, queste specifiche sono solitamente scritte su un'etichetta situata sull'obiettivo.

Passaggio 3. Calcolo di hio.
Dopo aver calcolato do e Dio, è possibile calcolare l'altezza dell'oggetto ingrandito e l'ingrandimento dell'obiettivo. Notare i due segni di uguale nell'equazione di ingrandimento dell'obiettivo (M = (hio/ho) = -(dio/Do)) - questo significa che tutte le parti di questa equazione sono uguali tra loro, quindi possiamo calcolare M e hio nell'ordine che vogliamo.
-
Per questo problema di esempio, possiamo calcolare hio come questo:
-
- (hio/ho) = -(dio/Do)
- (hio/6) = -(33, 3/50)
- hio = -(33, 3/50) x 6
- hio = - 3, 996 cm
-
- Nota che l'altezza dell'oggetto qui è negativa, il che indica che l'immagine che vedremo in seguito sarà invertita (alto-basso).

Passaggio 4. Calcolo di M
Puoi calcolare l'ultima variabile con l'equazione -(dio/Do) o (hio/ho).
-
Nell'esempio seguente, come calcolare M è il seguente:
-
- M = (hio/ho)
- M = (-3, 996/6) = - 0, 666
-
-
Il risultato sarà lo stesso anche se calcolato utilizzando il valore di d:
-
- M = -(dio/Do)
- M = -(33, 3/50) = - 0, 666
-
- Si noti che lo zoom non ha un'etichetta di unità.
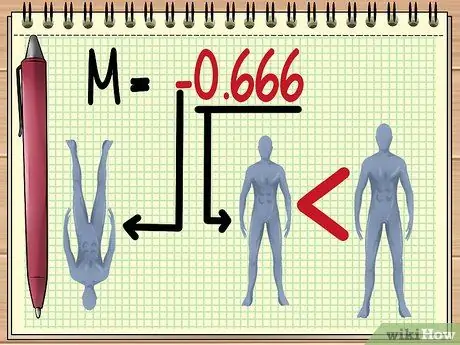
Passaggio 5. Comprensione del valore M
Una volta ottenuta la grandezza del valore M, puoi stimare diverse cose sull'immagine che vedrai attraverso l'obiettivo, vale a dire:
-
La dimensione.
Maggiore è il "valore assoluto" di M, più grande sarà l'oggetto visualizzato con l'obiettivo. Il valore M compreso tra 0 e 1 indica che l'oggetto sembrerà più piccolo.
-
Orientamento agli oggetti.
Un valore negativo indica che l'immagine formata verrà invertita.
- Nell'esempio qui riportato, il valore M di -0,666 significa che, in base al valore della variabile esistente, sarà visibile l'ombra della bambola. capovolto e due terzi più piccolo della dimensione effettiva.
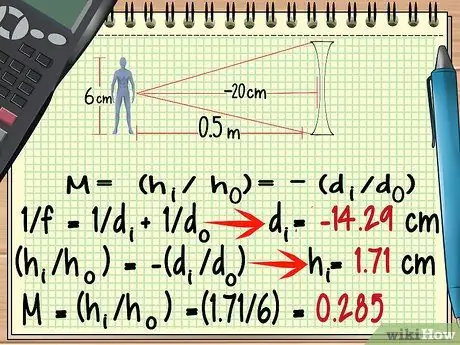
Passaggio 6. Per una lente divergente, utilizzare un punto focale negativo
Sebbene la forma di una lente divergente sia molto diversa da quella di una lente convergente, puoi calcolarne l'ingrandimento utilizzando la stessa formula di cui sopra. Le eccezioni da tenere a mente sono Il punto focale della lente divergente è negativo.
Nel problema di esempio sopra, questo influenzerà la risposta che otterrai calcolando dio, quindi assicurati di prestare attenzione a questo.
-
Risolviamo il problema di esempio sopra, solo che ora usiamo una lente divergente con lunghezza focale - 20cm.
Le altre variabili rimangono lo stesso valore.
-
Prima di tutto, calcoleremo dio usando l'equazione della lente:
-
- 1/f = 1/do + 1/dio
- 1/-20 = 1/50 + 1/dio
- -5/100 - 2/100 = 1/dio
- -7/100 = 1/dio
- -100/7 = dio = - 14, 29 cm
-
-
Ora calcoleremo hio e M con un valore di dio quello nuovo.
-
- (hio/ho) = -(dio/Do)
- (hio/6) = -(-14, 29/50)
- hio = -(-14, 29/50) x 6
- hio = 1, 71 cm
- M = (hio/ho)
- M = (1, 71/6) = 0, 285
-
Metodo 2 di 2: Calcolo dell'ingrandimento di più obiettivi
Metodo semplice a due lenti
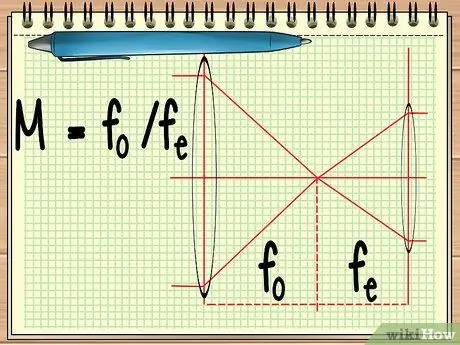
Passaggio 1. Calcola il punto focale delle due lenti
Quando si utilizza uno strumento composto da due lenti affiancate (come un telescopio o un binocolo), tutto quello che bisogna scoprire è il punto focale delle due lenti per calcolare l'ingrandimento complessivo delle due lenti. questo può essere calcolato con la semplice equazione M = fo/Fe.
Nell'equazione, fo è il punto focale della lente dell'obiettivo e fe è il punto focale dell'oculare. La lente dell'obiettivo è la lente grande che si trova vicino all'oggetto, mentre la lente oculare è la lente che si trova vicino all'occhio dell'osservatore.

Passaggio 2. Inserisci le informazioni che hai già nell'equazione M = fo/Fe.
Una volta che hai i punti focali di entrambe le lenti, è molto facile calcolarli, - calcola il rapporto dividendo la lunghezza focale della lente dell'obiettivo per la lunghezza focale dell'oculare. La risposta che ottieni è l'ingrandimento totale dello strumento.
-
Ad esempio, supponiamo un semplice telescopio, è scritto che il punto focale della lente dell'obiettivo è 10 cm e il punto focale dell'oculare è 5 cm, quindi l'ingrandimento è 10/5 = 2.
Metodo complicato
Passaggio 1. Calcolare la distanza tra le lenti e l'oggetto
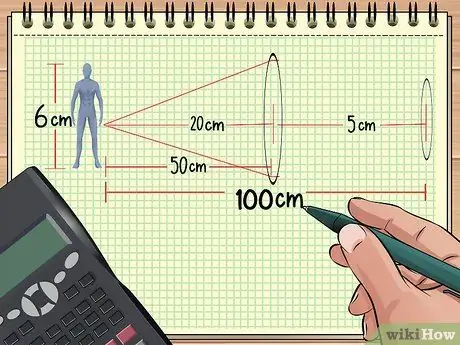
Se hai due lenti disposte in fila davanti a un oggetto, l'ingrandimento totale può essere calcolato se conosci la distanza dalle lenti all'oggetto, la dimensione dell'oggetto e il punto focale delle due lenti. Si può calcolare anche il resto.
Ad esempio, supponiamo di disporre oggetti e lenti come nel problema di esempio 1 sopra: una bambola è a 50 cm da una lente convergente che ha una lunghezza focale di 20 cm. Ora, posiziona la seconda lente con punto focale 5 cm a una distanza di 50 cm dalla prima lente (100 cm dalla bambola). Dopodiché, calcoleremo l'ingrandimento totale utilizzando le informazioni che abbiamo ottenuto
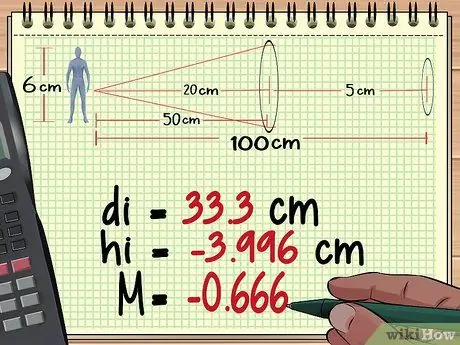
Passaggio 2. Calcola la distanza dell'oggetto, l'altezza e l'ingrandimento dall'obiettivo 1
La prima parte del calcolo dell'ingrandimento di più obiettivi è la stessa del calcolo dell'ingrandimento di un singolo obiettivo. Inizia con l'obiettivo più vicino all'oggetto, usa l'equazione dell'obiettivo per trovare la distanza dall'immagine formata, quindi usa l'equazione di ingrandimento per trovare l'altezza e l'ingrandimento dell'immagine. Fare clic qui per visualizzare altri calcoli di ingrandimento dell'obiettivo singolo.
-
Dai nostri calcoli nel Metodo 1 sopra, troviamo che il primo obiettivo produce un'immagine alta quanto - 3, 996 cm, distanza 33,3 cm dietro l'obiettivo e con un ingrandimento di - 0, 666.
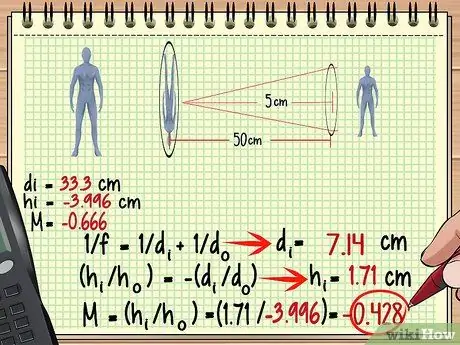
Passaggio 3. Utilizzare l'immagine della prima lente come oggetto della seconda lente
Ora, trovare l'ingrandimento, l'altezza e altro per il secondo obiettivo è molto semplice: usa solo lo stesso metodo che hai usato per il primo obiettivo, questa volta tratta l'immagine come un oggetto. Ricorda che la distanza dell'immagine dalla seconda lente non è sempre uguale alla distanza dell'oggetto dalla prima lente.
-
Nell'esempio sopra, poiché l'immagine si forma 33,3 cm dietro la prima lente, la distanza è 50-33,3 = 16,7 cm davanti alla seconda lente. Usiamo questa misura e la lunghezza focale della seconda lente per trovare l'immagine formata dalla seconda lente.
-
- 1/f = 1/do + 1/dio
- 1/5 = 1/16, 7 + 1/dio
- 0, 2 - 0, 0599 = 1/dio
- 0, 14 = 1/dio
- Dio = 7, 14 cm
-
-
Ora possiamo calcolare hio e M per la seconda lente:
-
- (hio/ho) = -(dio/Do)
- (hio/-3, 996) = -(7, 14/16, 7)
- hio = -(0, 427) x -3, 996
- hio = 1, 71 cm
- M = (hio/ho)
- M = (1, 71/-3, 996) = - 0, 428
-
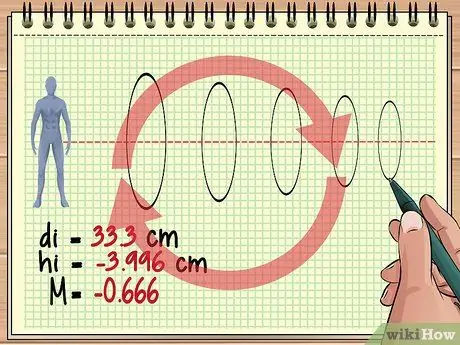
Passaggio 4. Continua a calcolare in questo modo per gli obiettivi aggiuntivi
Questo approccio di base è lo stesso se ci sono tre, quattro o centinaia di lenti allineate davanti a un oggetto. Per ogni obiettivo, considera l'immagine dell'obiettivo precedente come oggetto e usa l'equazione dell'obiettivo e l'equazione dell'ingrandimento per trovare la risposta che desideri.
Tieni presente che ogni obiettivo successivo può invertire continuamente l'immagine formata. Ad esempio, il valore di ingrandimento che abbiamo ottenuto in precedenza (-0, 428) indica che l'immagine che vedremo è circa 4/10 della dimensione effettiva dell'oggetto, ma perpendicolare, perché l'immagine dell'obiettivo precedente è invertita
Suggerimenti
- I binocoli di solito forniscono una spiegazione delle specifiche di ingrandimento sotto forma di un numero per un altro numero. Ad esempio, il binocolo può essere specificato come 8x25 o 8x40. Se scritto così, il primo numero è l'ingrandimento del binocolo. Poco importa anche se nell'esempio riportato i due numeri sono diversi in grandezza, entrambi i binocoli hanno un ingrandimento di 8 volte. Il secondo numero indica quanto chiara sarà formata l'immagine dal binocolo.
- Ricorda che per le lenti a lente singola, l'ingrandimento sarà negativo se la distanza dell'oggetto è maggiore della lunghezza focale dell'obiettivo. Ciò non significa che l'immagine formata sarà più piccola. In questo caso, l'ingrandimento avviene ancora, ma l'immagine formata sarà vista capovolta (top-down) dall'osservatore.






