- Autore Jason Gerald [email protected].
- Public 2023-12-16 11:19.
- Ultima modifica 2025-01-23 12:21.
Se hai già capito, convertire le frazioni ordinarie in decimali non è difficile. Per convertire frazioni comuni in decimali, puoi usare una divisione lunga, una moltiplicazione o anche una calcolatrice se non vuoi calcolare a mano. Una volta padroneggiato il metodo, sarai in grado di convertire facilmente le frazioni in decimali.
Fare un passo
Metodo 1 di 4: con divisione lunga
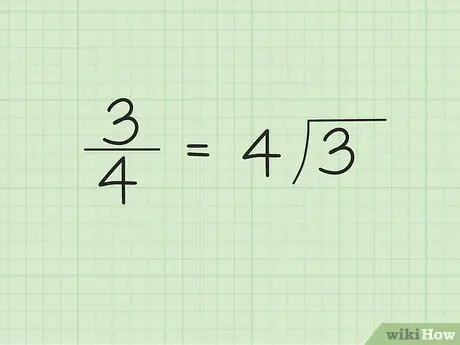
Passaggio 1. Scrivi il denominatore all'esterno/lato sinistro del simbolo del divisore e il numeratore all'interno/lato destro del simbolo del divisore
Ad esempio, supponiamo di voler convertire 3/4 in un decimale. Scrivere “4” all'esterno/a sinistra del simbolo del divisore e “3” all'interno/a destra del simbolo del divisore. "4" è il numero che divide e "3" è il numero che viene diviso.

Passaggio 2. Scrivi "0", quindi un punto decimale (una virgola), sopra il simbolo del divisore
Poiché è una frazione che conta, il risultato deve essere inferiore a uno, quindi questo passaggio è molto importante. Successivamente, scrivi il segno decimale, quindi "0", dopo il numero "3" all'interno/a destra del simbolo del divisore. Anche se "3" è uguale a "3, 0", lo zero consente di dividere "3, 0" per "4".

Passaggio 3. Calcola la risposta utilizzando una divisione lunga
Con la divisione lunga, per ora, il segno decimale può essere ignorato, quindi devi solo calcolare 30 diviso per 4. Ecco come:
- Innanzitutto, dividi 3, 0, che conta come 30, per 4. Il valore da 4 a 30 più vicino è 4 x 7 = 28, lasciando 2. Quindi, scrivi "7" dopo "0", sopra il divisore e "28" sotto " 3, 0” dentro/a destra del simbolo del divisore. Sotto 28, scrivi "2", il resto di 30 meno 28.
- Quindi, scrivere "0" dopo "3, 0" in modo che diventi "3, 00", che può essere considerato come "300", all'interno/a destra del simbolo del divisore. Quindi, 0 può essere abbassato a destra di "2" in modo che "20" sia divisibile per "4".
- “20” diviso per “4” è uguale a “5”. Quindi, scrivi "5" dopo "0,7" sopra il simbolo del divisore in modo che diventi "0,75".

Passaggio 4. Scrivi la risposta finale
Quindi, "3" diviso per "4" è uguale a "0,75". Scrivi la risposta. Finito.
Metodo 2 di 4: Frazioni che generano decimali ripetuti
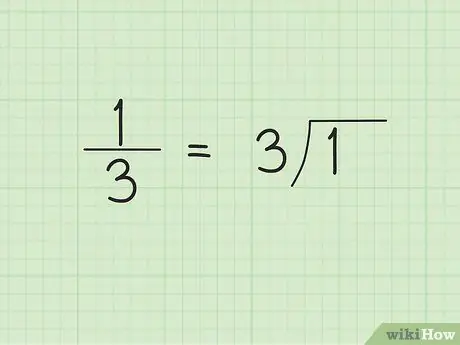
Passaggio 1. Crea una divisione lunga
Quando inizi una divisione a cifre lunghe, potresti non essere in grado di prevedere che il risultato sarà un numero decimale ripetuto. Ad esempio, supponiamo di voler convertire la frazione comune 1/3 in forma decimale. Scrivi 3, o il denominatore, sul lato esterno/sinistro del simbolo del divisore e 1 sul lato interno/destro del simbolo del divisore.

Passaggio 2. Scrivi uno 0, quindi un segno decimale, sopra il simbolo del divisore
Poiché il risultato deve essere minore di 1, questo passaggio prepara la risposta da scrivere in forma decimale. Il segno decimale deve essere scritto anche a destra del numero “1” che si trova all'interno/a destra del simbolo del divisore.
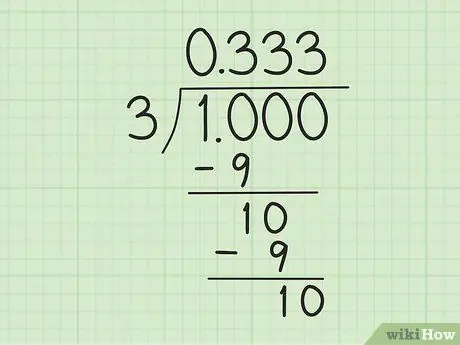
Passaggio 3. Inizia a calcolare la divisione lunga
Inizia facendo "1" in "1, 0", che conta come "10", in modo che sia divisibile per "3". Quindi, eseguire i seguenti passaggi:
- Dividi 10 per 3. Usa 3 x 3 = 9 per fare il resto di 1. Quindi scrivi 3 a destra dello "0", sopra il simbolo del divisore e sottrai 10 per 9 per ottenere il resto di 1.
- Scrivi uno "0" a destra del numero "1" (il resto di 10 meno 9 nel passaggio precedente) qui sotto per ottenere un altro "10". Quando si divide nuovamente "10" per "3", si ripete lo stesso processo: scrivere "3" a destra del primo "3" sopra il simbolo del divisore e sottrarre il nuovo "10" per "9".
- Continua finché non si forma un motivo. Sai che c'è qualcosa di strano? Questa divisione può andare avanti per sempre. 10 è sempre divisibile per 3: ci sarà sempre un "1" in basso e un nuovo "3" dopo la virgola sopra il simbolo del divisore.
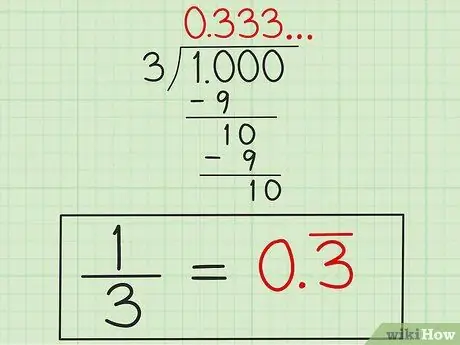
Passaggio 4. Scrivi la risposta
Dopo aver saputo che "3" si ripeterà, scrivi la risposta come "0, 3" con una riga sopra il numero "3" (o "0, 33" con una riga sopra entrambi i numeri "3") per indicare che il numero "3" continua a ripetersi. Questa risposta è nella forma decimale 1/3 perché 1 diviso per 3 non finirà da solo.
Ci sono molte frazioni che producono decimali ripetuti, come 2/9 ("0, 2" con "2" ripetuto), 5/6 ("0, 83" con "3" ripetuto) o 7/9 ("0, 83" con "3" ripetuto), 7” con “7” continua a ripetersi). Questo schema si verifica sempre quando il denominatore è un multiplo di 3 e il numeratore non può essere divisibile per il denominatore
Metodo 3 di 4: per moltiplicazione

Passaggio 1. Trova il numero che può essere moltiplicato per il denominatore della frazione per produrre 10, 100, 1.000 o qualsiasi numero in base 10
Questo può essere un modo semplice per convertire le frazioni in decimali senza usare una divisione lunga o una calcolatrice. Innanzitutto, trova un numero che può essere moltiplicato per il denominatore della frazione per ottenere 10, 100, 1.000 e così via. Per farlo, dividi prima 10, poi 100, poi 1.000 e così via per il denominatore finché non ottieni un numero intero. Esempio:
- 3/5. 10/5 = 2.2 è un numero intero. 2 può essere moltiplicato per 5 per ottenere 10. Quindi, 2 può essere utilizzato.
- 3/4. 10/4 = 2, 5. 2, 5 non è un numero intero. 100/4 = 25. 25 è un numero intero. 25 può essere moltiplicato per 4 per ottenere 100. Quindi 25 può essere utilizzato.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1.000/16 = 62, 5, 10.000/16 = 625. 625 è il primo numero intero ottenuto. 625 può essere moltiplicato per 16 per ottenere 10.000. Quindi, è possibile utilizzare 625.
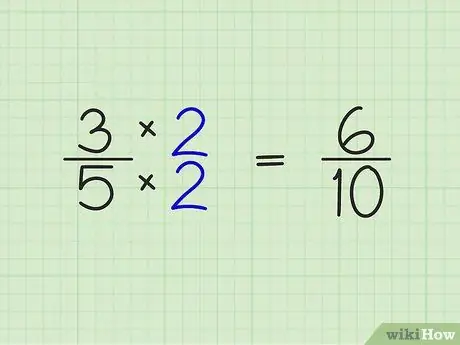
Passaggio 2. Moltiplica il numeratore e il denominatore della frazione per il numero intero ottenuto nel passaggio precedente
Questo passaggio è abbastanza facile. Basta moltiplicare i numeri sopra e sotto la frazione per il numero intero ottenuto nel passaggio precedente. Esempio:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3,125/10000

Passaggio 3. Scrivi la risposta finale
La risposta è che il numeratore è contrassegnato con un decimale in base al numero di 0 nel denominatore. Conta quanti 0 ci sono al denominatore. Se c'è solo 1 0 nel denominatore, sposta il punto decimale a sinistra di 1 cifra e così via. Esempio:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Metodo 4 di 4: con calcolatrice

Passaggio 1. Dividi il numeratore per il denominatore
Questo metodo è molto semplice. Basta usare una calcolatrice per dividere il numeratore, il numero in cima alla frazione, per il denominatore, il numero in fondo alla frazione. Ad esempio, supponiamo di voler convertire 3/4 in un decimale. Basta premere "3", quindi il simbolo di divisione ("÷'"), quindi "4" e infine il simbolo di uguale ("=").

Passaggio 2. Annota le risposte che ottieni
La risposta è 0,75, quindi la forma decimale della frazione comune 3/4 è 0,75.
Suggerimenti
- Per verificare se la tua risposta è corretta, moltiplica la risposta per il denominatore della frazione. Se la tua risposta è corretta, il prodotto della moltiplicazione è il numeratore della frazione.
- Alcune frazioni possono essere convertite in decimali creando frazioni comparabili i cui denominatori sono in base 10 (10, 100, 1.000 e così via). Quindi, usa i valori posizionali per annotare la forma decimale corretta.






