- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:19.
- Ultima modifica 2025-01-23 12:21.
Per la maggior parte delle persone, le frazioni sono i primi calcoli complicati che si incontrano. Il concetto di frazioni è piuttosto difficile e richiede l'apprendimento di condizioni speciali per farlo. Poiché le frazioni hanno regole speciali per l'addizione, la sottrazione, la moltiplicazione e la divisione, molte persone sono confuse al riguardo. Tuttavia, con molta pratica, chiunque può imparare e completare i calcoli relativi alle frazioni.
Fare un passo
Metodo 1 di 5: comprensione delle frazioni
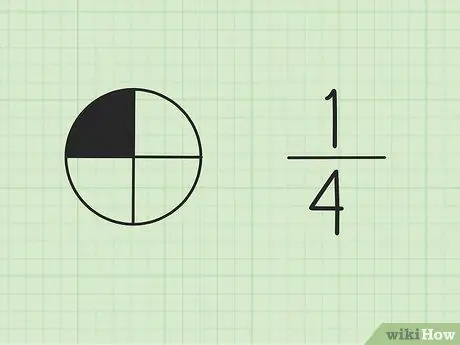
Passaggio 1. Comprendi che le frazioni fanno parte di un tutto
Il numero in alto si chiama numeratore e rappresenta il numero di parti del totale. Il numero in basso è chiamato denominatore, che rappresenta il numero totale di parti.
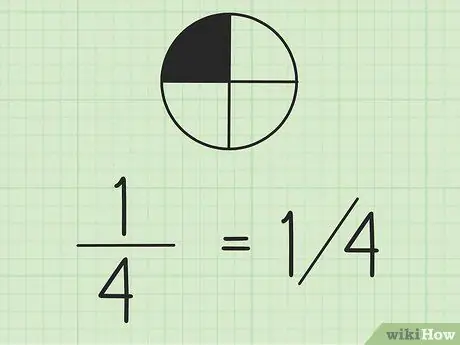
Passaggio 2. Tieni presente che puoi scrivere le frazioni usando le barre
Il numero a sinistra è il numeratore e il numero a destra è il denominatore. Se stai lavorando con le frazioni sulla stessa riga, è una buona idea scrivere il numeratore sopra il denominatore.
Ad esempio, se prendi una delle quattro fette di pizza, hai la pizza. Se hai 7/3 pizze, significa che hai due pizze intere più 1 di 3 fette di pizza
Metodo 2 di 5: differenza tra frazioni miste e semplici

Passaggio 1. Comprendere che i numeri misti sono costituiti da numeri interi e frazioni, ad esempio 2 1/3 o 45 1/2
Di solito, devi convertire i numeri misti in una forma più semplice per aggiungere, sottrarre, moltiplicare o dividere.

Passaggio 2. Modificare il numero misto moltiplicando il numero intero per il denominatore nella frazione, quindi aggiungendolo per il numeratore
Scrivi il risultato come numeratore, mentre il denominatore non cambia.
Ad esempio, per convertire 2 1/3 in una semplice frazione, moltiplica 2 per 3, quindi aggiungi 1 e ottieni 7/3

Passaggio 3. Converti frazioni semplici in numeri misti dividendo il numeratore per il denominatore
L'intero risultato della divisione viene scritto come numero intero e il resto della divisione viene scritto come numeratore della frazione. Il denominatore non cambia.
Ad esempio, per convertire 7/3 in un numero misto, dividi 7 per 3 per ottenere 2 con il resto di 1. Quindi il numero misto è 2 1/3. Le frazioni semplici possono essere convertite in numeri misti solo se il numeratore è maggiore del denominatore
Metodo 3 di 5: aggiunta e sottrazione di frazioni
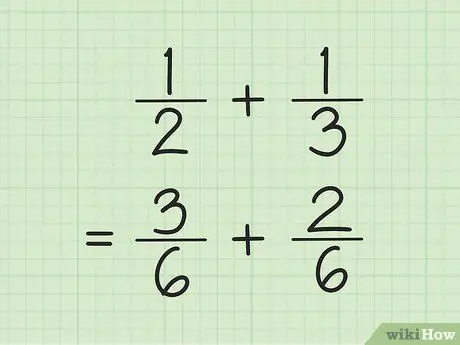
Passaggio 1. Trova un denominatore comune per aggiungere e sottrarre frazioni
Il trucco, moltiplica i numeri al denominatore, quindi moltiplica ogni numeratore per il numero utilizzato per trovare il denominatore. A volte, puoi trovare il MCM (minimo multiplo comune) per il denominatore moltiplicando i denominatori l'uno per l'altro.
Ad esempio, per aggiungere e 1/3, trova prima il MCM (minimo multiplo comune) dei due denominatori moltiplicando tra loro. Quindi, moltiplichi 2 e 3 per ottenere LCM 6. Moltiplica 1 per 3 per ottenere 3 come nuovo numeratore della prima frazione. Moltiplica 1 per 2 per ottenere 2 come nuovo numeratore della seconda frazione. Le tue nuove frazioni sono 3/6 e 2/6
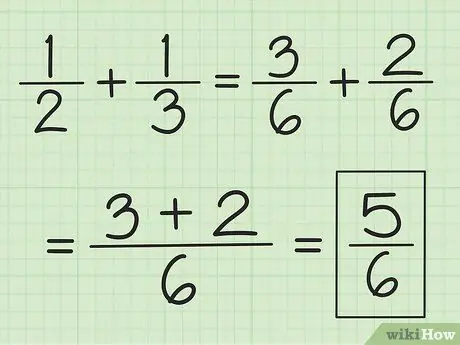
Passaggio 2. Somma i due numeratori e non modificare il denominatore
Ad esempio, 3/6 più 2/6 fa 5/6 e 2/6 più 1/6 fa 3/6
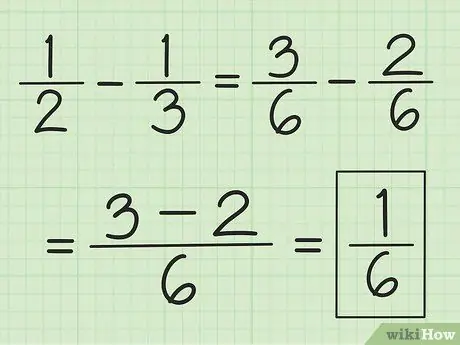
Passaggio 3. Utilizzare una tecnica simile per la sottrazione
Trova prima il MCM dei denominatori, ma invece di sommarli, sottrai il numero del primo numeratore per il numero del secondo.
Ad esempio, per sottrarre 1/3 da 1/2, cambia prima le frazioni in 3/6 e 2/6, quindi sottrai 3 per 2 per ottenere 1. Il risultato è 1/6
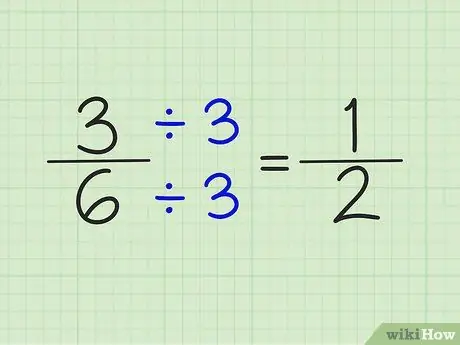
Passaggio 4. Semplifica le frazioni dividendo numeratore e denominatore per lo stesso numero
Ad esempio, il numero 5/6 non può essere semplificato. Tuttavia, 3/6 può essere semplificato dividendo numeratore e denominatore per il numero 3. Il risultato è una frazione di 1/2

Passaggio 5. Converti la frazione in un numero misto se il numeratore è maggiore del denominatore
Metodo 4 di 5: moltiplicare e dividere le frazioni
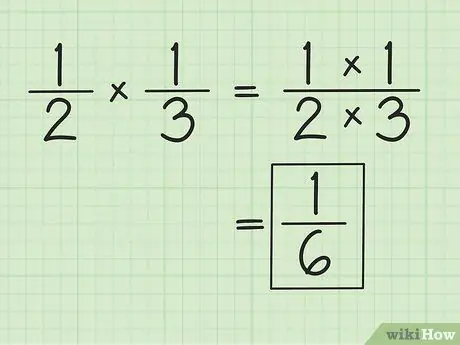
Passaggio 1. Moltiplicare numeratore e denominatore separatamente per moltiplicare le frazioni
Ad esempio, moltiplicando per 1/3, il risultato è 1/6 (1 per 1 e 2 per 3). Non è necessario abbinare i denominatori quando si moltiplicano le frazioni. Semplificare o modificare i risultati ottenuti, se necessario
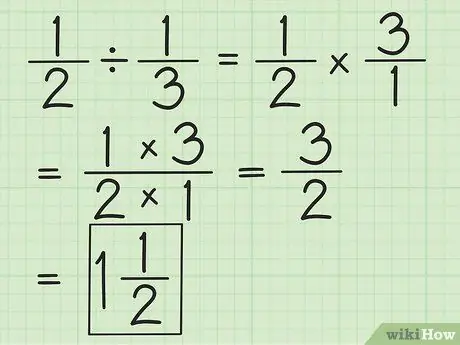
Passaggio 2. Dividi due frazioni invertendo la seconda frazione, quindi moltiplicando entrambe
Ad esempio, se vuoi dividere 1/2 per 1/3, prima inverti la seconda frazione in 3/1. Moltiplica per 3/1 e ottieni 3/2. Semplifica le frazioni o converti in numeri misti, se possibile
Metodo 5 di 5: lavorare con frazioni complesse
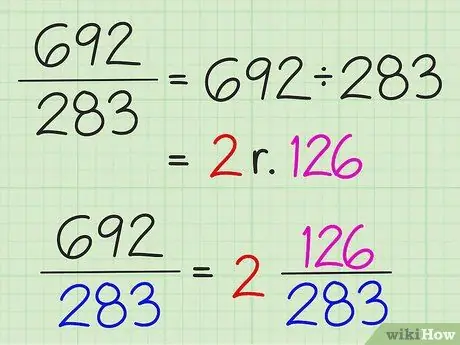
Passaggio 1. Lavora tutte le frazioni allo stesso modo, anche se il problema sembra molto complicato
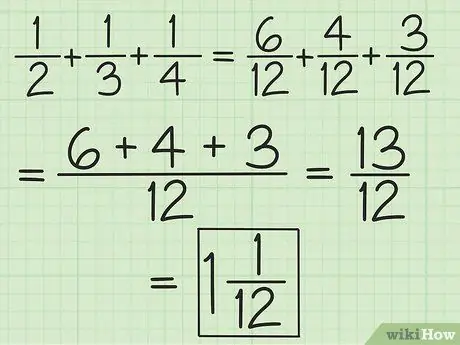
Passaggio 2. Abbina i denominatori per tutte le frazioni o lavora a coppie partendo da sinistra a destra per aggiungere e sottrarre più di due frazioni
Ad esempio, per sommare 1/2, 1/3 e 1/4, puoi cambiarli in 6/12, 4/12 e 3/12 per ottenere 13/12, oppure puoi aggiungere 3/6 e 2 /6 quindi ottieni 5/6, quindi aggiungi 5/6 e 1/4 (equalizza i denominatori in modo che la seconda frazione diventi 3/12) per ottenere 13/12 (10/12 più 3/12). Convertilo in un numero misto, che è 1 1/12
Suggerimenti
- Ricorda che hai imparato parecchia matematica. La matematica è come una lingua che puoi pronunciare fluentemente e ora stai cercando di imparare a leggerla e scriverla.
- Ricorda di semplificare sempre il risultato finale del tuo calcolo, indipendentemente dal fatto che il tuo problema sia sotto forma di frazione ordinaria, numero misto o frazione complessa.






