- Autore Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:19.
- Ultima modifica 2025-01-23 12:21.
Il conteggio delle frazioni è una delle abilità matematiche più utili da sviluppare. Prima di eseguire calcoli frazionari, impara a identificare parti e tipi di frazioni. Successivamente, puoi aggiungerli o sottrarli. Per calcoli più complessi, impara a moltiplicare e dividere le frazioni. Di solito, dovrai anche semplificare o ridurre le frazioni.
Fare un passo
Metodo 1 di 4: riconoscimento delle frazioni

Passaggio 1. Trova la frazione
Le frazioni sono scritte come un numero sopra la linea di divisione e un altro numero sotto la linea.
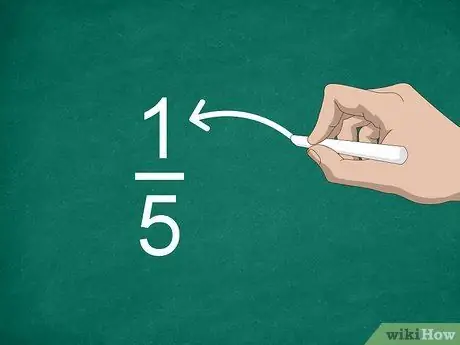
Passaggio 2. Identificare il numeratore
Il numero sopra la linea è chiamato numeratore e mostra quante parti ci sono nella frazione.
Ad esempio, nella frazione 1/5, "1" è il numeratore
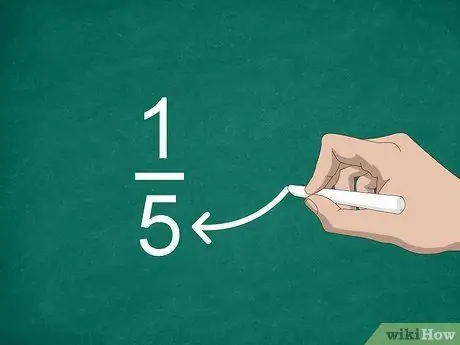
Passaggio 3. Trova il denominatore
Il numero posto sotto la linea è chiamato denominatore. Questo valore indica il numero di parti che "costruiscono" un intero.
Ad esempio, nella frazione 1/5, "5" è il denominatore, quindi ci sono cinque parti nella frazione

Passaggio 4. Determinare se le frazioni sono frazioni ragionevoli o frazioni improprie
Se il numeratore è minore del denominatore, la frazione è una frazione naturale. Nelle frazioni improprie il numeratore è maggiore del denominatore.
- Ad esempio, 3/4 è una frazione ragionevole e 5/3 è una frazione impropria.
- Se hai un numero intero che include una frazione, il numero è noto come numero misto. Ad esempio, 1 1/2 è un numero misto.
Metodo 2 di 4: aggiungere o sottrarre frazioni

Passaggio 1. Identifica le frazioni con lo stesso denominatore
Se devi aggiungere o sottrarre frazioni, ogni frazione deve avere lo stesso denominatore prima di eseguire il calcolo. Osserva il denominatore di ogni frazione per assicurarti che siano tutte uguali (simili).
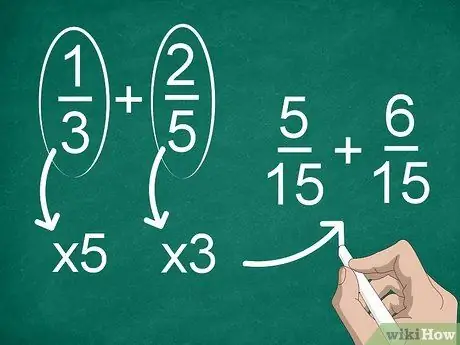
Passaggio 2. Trova un denominatore comune se ogni frazione ha un denominatore diverso
Se i denominatori non sono gli stessi, dovrai cambiare le frazioni per avere lo stesso denominatore. Per trovare un denominatore comune, moltiplica ogni frazione per il denominatore dell'altra.
Ad esempio, per trovare un denominatore comune in 1/3 + 2/5, moltiplicare "1" e "3" per "5", quindi moltiplicare "2" e "5" per "3". Ora hai l'aggiunta di 5/15 + 6/15. Successivamente, puoi calcolare le frazioni
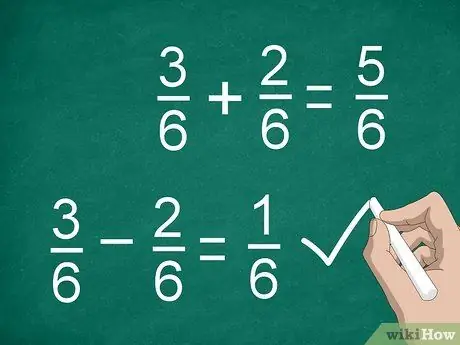
Passaggio 3. Aggiungere o sottrarre i numeratori per calcolare le frazioni
Una volta trovato un denominatore comune e moltiplicato i numeratori (se necessario), sei pronto per aggiungere o sottrarre. Aggiungi o sottrai i numeratori e posiziona il risultato sopra la linea di divisione. Scrivi il denominatore comune sotto la linea.
- Ad esempio, 3/6 - 2/6 = 1/6.
- Non aggiungere o sottrarre i denominatori.
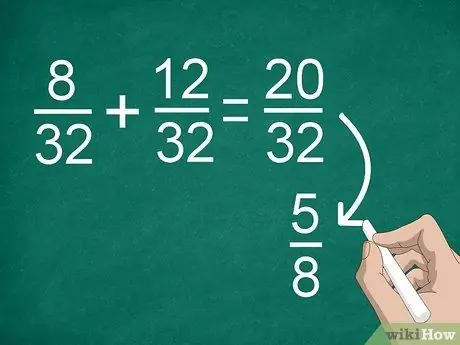
Passaggio 4. Semplificare i risultati, se necessario
Se in precedenza avevi bisogno di trovare un denominatore comune, potresti ottenere una frazione grande che puoi semplificare. Ad esempio, se aggiungi 8/32 +12/32, otterrai "20/32" come risultato. Questa frazione può essere semplificata in "5/8".
Metodo 3 di 4: Moltiplicare e semplificare le frazioni
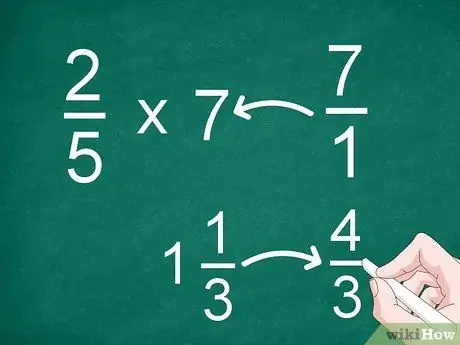
Passaggio 1. Converti frazioni miste o interi in frazioni improprie
Per rendere più facile la moltiplicazione, devi convertire ogni numero in una frazione ragionevole o impropria. Se hai numeri interi o misti che devono essere moltiplicati, convertili prima in una frazione comune (naturale o impropria).
- Ad esempio, per moltiplicare 2/5 per 7, converti "7" in una frazione. Successivamente, puoi moltiplicare 2/5 per 7/1.
- Se hai un numero misto come 1 1/3, convertilo in una frazione impropria ("4/3") prima di moltiplicare.
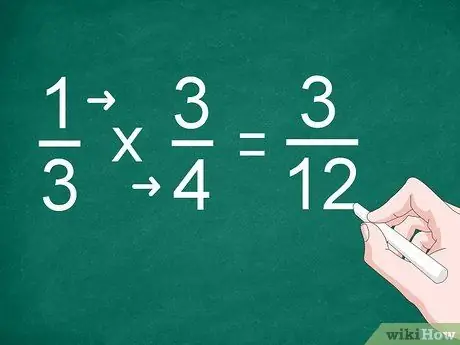
Passaggio 2. Moltiplica ogni numeratore e denominatore
Invece di fare addizioni, moltiplica il numeratore e scrivi il risultato sopra la linea di divisione. Devi anche moltiplicare i denominatori e scrivere il risultato sotto la linea.
Ad esempio, per moltiplicare 1/3 per 3/4, moltiplicare "1" per "3" per ottenere il numeratore. Moltiplica "3" per "4" per ottenere il denominatore. La risposta alla moltiplicazione è "3/12"

Passaggio 3. Semplifica i risultati
Di solito, dovrai ridurre il risultato a una forma più semplice, soprattutto se inizialmente hai frazioni innaturali. Trova il massimo comun divisore e usa quel fattore per semplificare numeratore e denominatore.
Ad esempio, per la frazione 3/12, il massimo comun divisore tra “3” e “12” è “3”. Dividi ogni elemento della frazione per "3" fino ad ottenere la frazione "1/4"
Metodo 4 di 4: dividere le frazioni
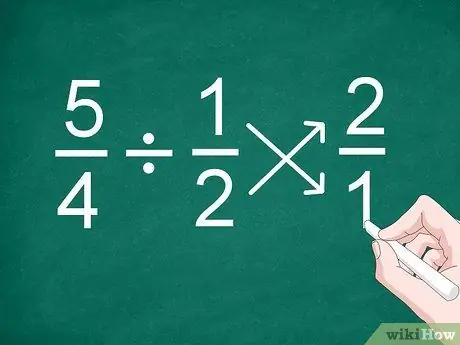
Passaggio 1. Invertire la posizione della seconda frazione
Il modo più semplice per dividere le frazioni, anche frazioni con denominatori diversi, è invertire la posizione della seconda frazione prima di calcolare il risultato.
Ad esempio, per il problema 5/4 1/2, invertire la posizione della frazione "1/2" per diventare "2/1"
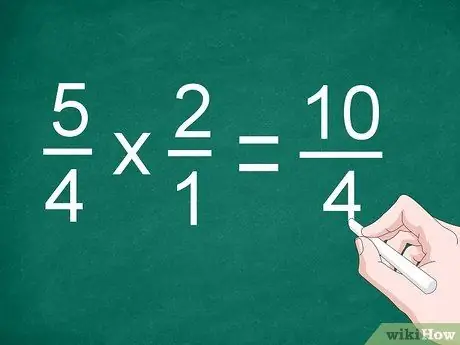
Passaggio 2. Moltiplica il numeratore e il denominatore
Moltiplicare le frazioni direttamente per moltiplicare i numeratori. Scrivi il risultato sopra la linea di divisione, quindi moltiplica il denominatore. Registra il prodotto dei denominatori sotto la linea.
Per l'esempio precedente, moltiplica 5/4 per 2/1 per ottenere "10/4"
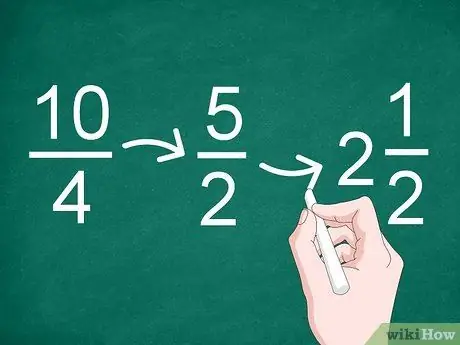
Passaggio 3. Semplificare i risultati, se necessario
Se il risultato della divisione è una frazione impropria o può essere ridotta, semplifica la frazione. Utilizzare il massimo comun divisore per ridurre la frazione.
- Ad esempio, il massimo comun divisore nella frazione 10/4 è "2", quindi il risultato della semplificazione diventa "5/2" (10 diviso 2 e 4 diviso 2).
- Poiché il risultato della semplificazione è una frazione impropria, puoi convertirla in un intero e in una frazione (un numero misto). Pertanto, 5/2 può essere modificato in "2".
Suggerimenti
- Se stai lavorando con frazioni complesse, dovrai eseguire alcuni passaggi aggiuntivi per semplificare la frazione. Tuttavia, questa stessa semplificazione è una parte obbligatoria del processo di calcolo.
- Scrivi sempre le frazioni in modo ordinato per ridurre il rischio di errori di calcolo.






